Das Konfidenzintervall in der Methodenvalidierung
Im heutigen Blogbeitrag wollen wir uns einmal mit der Rolle und den Anwendungsmöglichkeiten von Konfidenzintervallen (Synonym: Vertrauensintervall, Vertrauensbereich) bei der Methodenvalidierung beschäftigen.
Was wissen wir
In einem früheren Blogartikel haben wir beschrieben, was ein Konfidenzintervall / Vertrauensintervall ist. Wir wissen also, dass ein Konfidenzintervall einen Bereich umfasst, in dem sich bei unendlicher Messwiederholung mit einer gewissen Wahrscheinlichkeit (dem Konfidenzniveau) die wahre Lage eines Parameters, wie z.B. des Mittelwerts, also der „wahre Wert µ“, befindet. Er zielt damit auf die Präzision der Messung ab. Das Konfidenzniveau kann dabei z.B. mit 90, 95 oder 99% gewählt werden.
In unserem Beispiel zum Wirkstoffgehalt von Tabletten haben wir ausgerechnet, dass sich bei einem vorgegebenen Konfidenzniveau von 95% der echte Mittelwert zwischen der unteren (396,4 mg) und der oberen Grenze (401,2 mg) befindet. Dabei lagen eine Normalverteilung sowie eine zufällig gezogene und ausreichend große Stichprobe zu Grunde. Zudem haben wir gelernt, je höher wir das Konfidenzniveau anheben (z.B. von 90% auf 95%), desto breiter wird das Konfidenzintervall und desto mehr sinkt die Präzision. Was wir noch nicht gesagt hatten, ist, dass die Präzision ein Maß für den Standardfehler des Mittelwerts (standard error of the mean, SEM) einer Schätzung ist. In diesen spielen die Stichprobengröße n und die Streuung, also Standardabweichung σ, innerhalb der Population (und somit auch der Stichprobe) hinein, womit sich dann auch die Formel für die Berechnung des Konfidenzintervalls super verständlich erklären lässt [Anmerkung: z ist nicht der α-Fehler selbst, sondern der korrespondierende z-Wert]:
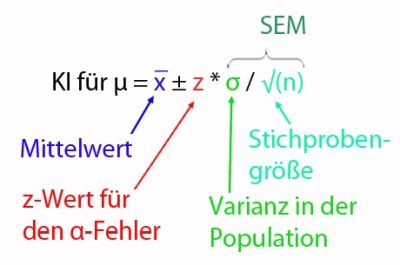
Noch eine kurze Anmerkung zum Wording: der α-Fehler wird auch als Irrtumswahrscheinlichkeit oder Signifikanzniveau bezeichnet. Er berechnet sich als 1- Konfidenzniveau (also z.B. 1 - 0,95 = 0,05 = 5%) und gibt uns Auskunft über das Restrisiko, mit unserer Beurteilung doch falsch zu liegen, also dass unser Konfidenzintervall den wahren Wert doch nicht enthält, wir aber „falsch-positiv“ davon ausgehen…
Was ist gefordert
Gemäß der derzeit gültigen Richtlinie ICH Q2(R1) von 1996 bzw. 2005 für die Validierung analytischer Methoden von Arzneimitteln und Wirkstoffen wird die Angabe von Konfidenzintervallen sowohl für die Richtigkeit als auch für alle Arten untersuchter Präzision gefordert.
Hinsichtlich der Validierung bioanalytischer Methoden ist die Angabe von Konfidenzintervallen weder in den derzeitigen Dokumenten der EMA, der FDA, der japanischen oder brasilianischen Gesundheitsbehörde gefordert, obwohl auch bei bioanalytischen Methoden ebenfalls Richtigkeit und Präzision zu untersuchende Validierungsparameter sind. Die entsprechenden Guidelines sind jedoch alle deutlich neueren Datums…
Im Rahmen einer Vielzahl von Methodenvalidierungen mit verschiedenen Kunden ist mir die explizite Angabe von Konfidenzintervallen nur bei einem Kunden über den Weg gelaufen, weil sein Kunde es gewünscht hat. Dort war dann je nach zu validierender Methode und Jahr für den Parameter Präzision alles vorhanden, von der jeweiligen Angabe von Konfidenzintervallen bei wirklich jeder Art von Präzision wie Wiederholpräzision, interner Laborpräzision und auch Reproduzierbarkeit (da 2 QC-Standorte beteiligt waren) bis hin zu einer einzelnen Angabe eines Konfidenzintervalls für eine „zusammenfassende Präzision“ (overall precision), komplett unabhängig von der Stichprobengröße. Womit wir beim Thema wären. In meinen Augen macht es aus statistischer Sicht nicht wirklich Sinn, ein Konfidenzintervall bei einer Stichprobe mit einem n von 6 (wie es bei der Wiederholpräzision üblicherweise der Fall ist) zu berechnen. Wie sinnvoll es für ein n von 9 (für die Richtigkeit mit 3 Replikaten bei 3 Konzentrationen) oder 12 (für die interne Laborpräzision mit 2 Analysten à 6 Replikaten an zwei Tagen) ist, mag jeder für sich entscheiden. Ab einer Stichprobe mit einem n von ≥ 15 ändert sich an der Breite eines Konfidenzintervalls jedoch nur noch wenig [1]. Aus diesem Grunde könnte es für eine „zusammenfassende Präzision“, die die Ergebnisse aller einzelnen Präzisionsuntersuchungen berücksichtigt, zumindest aus statistischer Sicht in Ordnung sein. Eine Angabe eines Konfidenzintervalls für die Richtigkeit ist mir nur in einem Fall begegnet und dann auch noch für jede Konzentration einzeln, sprich also je bei einem n von 3…
Unabhängig von meiner persönlichen Erfahrung, scheint zumindest die malaysische Gesundheitsbehörde Wert auf die Angabe eines Konfidenzintervalls für die Parameter Richtigkeit und Präzision bei analytischen Methodenvalidierungen zu legen oder gelegt zu haben…
Wann es Sinn macht
Starten wir mit einem Beispiel einer HPLC-Methode. Mit konstruierten Daten für die Präzision und die Richtigkeit könnte es so aussehen:
| Precision | Trueness | |||||||
|
Overall precision |
Relative peak area [Area%] | Level [%] |
Absolute peak areas [µAU*s] | Recovery [%] | ||||
| Measured data | Calculated data | |||||||
| Repea-tability | 1 | Day 1: operator 1 | 93.53 | 120 | 37106293 | 36727113 | 101 | |
| 2 | 93.68 | 37077541 | 101 | |||||
| 3 | 93.54 | 37330854 | 102 | |||||
| 4 | 93.55 | 110 | 34181732 | 33711289 | 101 | |||
| 5 | 93.58 | 33749143 | 100 | |||||
| 6 | 93.63 | 33893159 | 101 | |||||
| Inter-mediate precision | 1 | Day 1: operator 2 | 93.46 | 100 | 30047214 | 30695466 | 98 | |
| 2 | 93.22 | 30285204 | 99 | |||||
| 3 | 93.44 | 30030762 | 98 | |||||
| 1 | Day 2: operator 1 | 93.55 | 90 | 27863052 | 27679643 | 101 | ||
| 2 | 93.50 | 27549713 | 100 | |||||
| 3 | 93.54 | 27499621 | 99 | |||||
| 1 | Operator 1: equipment 2 | 93.42 | 80 | 23724539 | 24663819 | 96 | ||
| 2 | 93.48 | 23633961 | 96 | |||||
| 3 | 92.95 | 23871057 | 97 | |||||
| Mean [Area%] | 93.54 | Mean [%] | 99.23 | |||||
| SD [Area%] | 0.25 | SD [%] | 1.93 | |||||
| RSD [%] | 0.27 | RSD [%] | 1.92 | |||||
| 95% CI [Area%] | 93.41 to 93.66 | 95% CI [%] * | 98.25 to 100.20 | |||||
* siehe Update unten am Ende des Texts
Obwohl hierbei alle Daten inklusive der Konfidenzintervalle angegeben sind, steht man nun vor der Frage, was man damit anfangen kann oder was es bringen soll. Wenn ein Konfidenzintervall wie im Bespiel gezeigt z.B. für eine „zusammenfassende Präzision“ ermittelt wurde, so könnte dieses genutzt werden, um den Arbeitsbereich, der sich ja aus den Ergebnissen der Linearität, Richtigkeit und Präzision ableiten lässt, zu verfeinern, indem besonderes Augenmerk auf den kleinsten und größten Wert gelegt wird. Zudem kann eine Bestimmung von Konfidenzintervallen basierend auf den Präzisionsdaten z.B. bei der Untersuchung verschiedener Intermediate eines Herstellungsprozesses helfen, zu überprüfen, inwiefern die Methode zur Analyse all dieser Intermediate geeignet ist.
Das erscheint einleuchtend, doch der Sinn und Nutzen eines Konfidenzintervalls für die Wiederfindungsrate (recovery), also für die Richtigkeit, ist mir leider immer noch nicht klar… Irgendwo im Zuge der Recherche für diesen Artikel habe ich zwei interessante Dinge gelesen:
- “Confidence interval: The precision of findings”
- “Confidence intervals are focused on precision of estimates — confidently use them for that purpose!”
Dies legt mir den Schluss nahe, dass Konfidenzintervalle nicht unbedingt auf die Richtigkeit anzuwenden sind…
Ansonsten kann die Angabe bzw. Untersuchung von Daten mit Hilfe eines Konfidenzintervalls in einigen Fällen bei der Linearität Sinn machen, z.B. falls gewünscht bzw. bekannt ist, dass der y-Achsenschnittpunkt durch 0 verläuft, kann dies mit Hilfe eines Konfidenzintervalls abgeprüft werden. Oder – für den Statistik-begeisterten Analytiker – kann im Rahmen einer Residuenanalyse geschaut werden, ob die Residuen normal verteilt innerhalb des 95%-Lilliefors-Konfidenzintervalls in einem Normal-Quantil-Plot liegen.
Auch als Akzeptanzkriterium kann ein Konfidenzintervall sinnvoll sein, z.B. bei Untersuchungen zur Robustheit einer HPLC-Methode, von der man weiß, wo der Mittelwert liegt und was als Konfidenzintervall einzuhalten ist. In dem Fall kann man einfach prüfen, ob die unter den veränderten Bedingungen (z.B. veränderter pH-Wert der mobilen Phase) erhaltenen Mittelwerte im bekannten Konfidenzintervall liegen oder nicht. Genauso verhält es sich, wenn für die Robustheit einer TOC-Bestimmung untersucht werden soll, ob eine lange Lagerungsdauer der Proben einen Einfluss auf die Ergebnisse hat, indem überprüft wird, ob die Ergebnisse der lang gelagerten Proben im Konfidenzintervall einer zuvor analysierten frisch gezogenen Probe liegen. Ähnlich wäre es bei einer SDS-PAGE, bei der ein neuer Referenzstandard eingeführt werden soll. Hinsichtlich der Spezifität könnte als Akzeptanzkriterium definiert werden, dass der Mittelwert der Hauptbande des neuen Standards natürlich im Konfidenzintervall des alten bekannten Standards liegen soll. Für Validierungen bioanalytischer Methoden wird der Nutzen von Konfidenzintervallen beispielsweise im Zusammenhang mit Stabilitätsuntersuchungen beschrieben [2].
Eine weitere Anwendung können Konfidenzintervalle im Zuge der Überprüfung der Methodenfähigkeit (method capability) auf die Einhaltung der Grenzen der Spezifikation haben, falls dabei nicht die üblicherweise 6-fache Standardabweichung verwendet wird. Doch hier detaillierter darauf einzugehen würde den Rahmen sprengen ;-)
Fazit
Trotz der Forderung der Angabe von Konfidenzintervallen für die Präzision und die Richtigkeit in der ICH Q2(R1)-Richtlinie scheint die Umsetzung dieser Anforderungen bei Methodenvalidierungen nicht unbedingt von jeder Behörde erwartet zu werden, was aus statistischer Sicht absolut berechtigt ist. Dennoch gibt es auch bei Methodenvalidierungen Möglichkeiten, Konfidenzintervalle sinnvoll einzusetzen, z.B. bei Bestimmungen zur Robustheit.
Update 04.09.2019
Aufgrund nützlicher Kommentare nach Einstellung dieses Artikels bei Linkedin sollte die Berechnungsformel korrigiert bzw. präzisiert werden: für kleine Stichproben, wie das hier bei Methodenvalidierungen der Fall ist, sollte anstatt der z-Statistik die t-Statistik für die Berechnung des Konfidenzintervalls angewandt werden. Die z-Statistik wird bei größeren Stichproben (n > 30) angewandt und ist ein Spezialfall der t-Verteilung bei einer unendlichen Anzahl an Freiheitsgraden.
Außerdem sollte betont werden, dass bei einer Angabe eines Konfidenzintervalls das Konfidenzniveau sowie die Stichprobengröße mitanzugeben sind.
Im Hinblick auf die Richtigkeit wurde mir mitgeteilt, dass die Konfidenzintervalle für jede Konzentration einzeln zu berechnen seien. Dies bedeutet jedoch, dass jeweils nur ein n von 3 zu Grunde liegt, womit eine Berechnung in meinen Augen keinen Sinn macht…
Referenzen
[1] Ellison S.L.R., Barwick V.J., Duguid Farrant T.J. (2009). Practical Statistics for the Analytical Scientist: A Bench Guide, 2nd edition, RSC Publishing, ISBN: 978-0-85404-131-2, Kapitel 9.2.2.1
[2] Rudzki P.J., Leś A. (2008). Application of confidence intervals to bioanalytical method validation – drug stability in biological matrix testing, Acta Pol Pharm., Vol. 65 (6): 743-747
