Linearitätstests
Bei vielen analytischen Methoden ist eine Kalibrierung zur Ermittlung des linearen Bereichs erforderlich. Um zu überprüfen, ob die ermittelte Kalibrierfunktion auch wirklich linear ist, können Linearitätstests angewendet werden.
Je nach Geschäftsbereich ist die Überprüfung der Linearität mit Hilfe eines Linearitätstests auch bei Methodenvalidierungen gefordert oder könnte zumindest sinnvoll sein. In einem früheren Beitrag haben wir uns in diesem Zusammenhang einmal die relative Response angesehen.
Zwischenzeitlich sind mir jedoch weitere Linearitätstests über den Weg gelaufen und diesen wollen wir uns im heutigen Beitrag widmen.
Linearitätstest: „Punkt-zu-Punkt-Steigung“
Der Linearitätstest mit „Punkt-zu-Punkt-Steigung“ hat mich ein wenig an den Berechnungsweg der relativen Response erinnert. Er wird z.B. in der aktuellen DIN 38402-51 (von 2017) beschrieben, wo er den von älteren Normen empfohlenen Linearitätstest nach Mandel ersetzt. Dabei sind mind. 6 Konzentrationen äquidistant verteilt erforderlich und es werden aus den Datenpaaren von je 2 aufeinanderfolgenden Messpunkten die Steigungen berechnet. Danach wird - abweichend zur Berechnung der relativen Response nicht der Mittelwert - sondern der Median berechnet und die Einzelwerte mit den auf den Median angewandten Toleranzgrenzen verglichen, wobei die Darstellung auch hier mit Hilfe einer Qualitätsregelkarte erfolgt.
An einem Beispiel einer photometrischen Nitritbestimmung sieht das so aus (das Beispiel ist der DIN 38402-51 entnommen), dabei ist eine 10%ige Toleranz angewendet worden:
| Nr. Kalibrierstandard | Konzentration (xi) [µg/L] | Extinktion (yi) [-] | Punkt-zu-Punkt Steigung (Δy/Δx) [1/µg*L-1] | Abweichung vom Median [1/µg*L-1] |
| 1 | 0,66 | 0,0037 | 0,00712 | -0,00023 |
| 2 | 1,32 | 0,0084 | 0,00735 | 0,00000 |
| 3 | 2,64 | 0,0181 | 0,00702 | -0,00033 |
| 4 | 5,26 | 0,0365 | 0,00712 | -0,00023 |
| 5 | 6,58 | 0,0459 | 0,00720 | -0,00015 |
| 6 | 7,90 | 0,0554 | 0,00733 | -0,00002 |
| 7 | 10,60 | 0,0752 | 0,00736 | 0,00001 |
| 8 | 26,00 | 0,1885 | 0,00777 | 0,00042 |
| 9 | 44,71 | 0,3339 | 0,00836 | 0,00101 |
| 10 | 63,19 | 0,4884 | 0,00901 | 0,00166 |
| 11 | 82,18 | 0,6595 | 0,01003 | 0,00269 |
| 12 | 100,00 | 0,8383 | - | - |
| Median | 0,00735 | - | ||
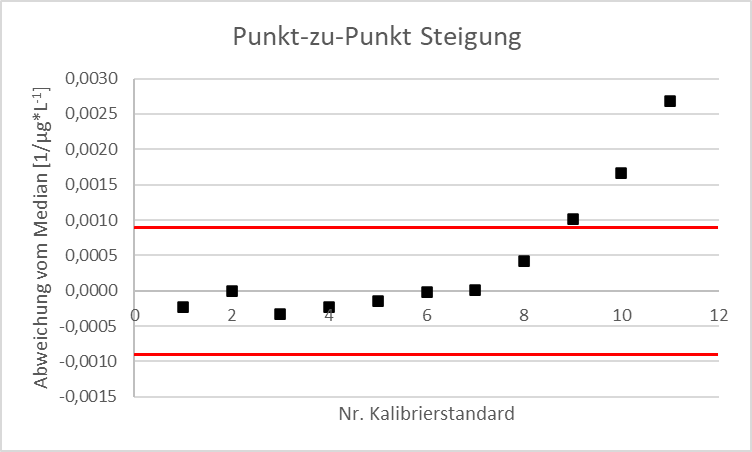
Unter Berücksichtigung der 10%igen Toleranz ist die Aussage, dass die Linearität nach dem 8. Kalibrierstandard endet, sich der Kalibrierbereich also nur von 0,66 – 26,00 µg/L erstreckt.
Empirischer Krümmungstest
Neben dem eben erläuterten Linearitätstest mit „Punkt-zu-Punkt-Steigung“ wird in der DIN 38402-51 außerdem der empirische Krümmungstest behandelt. Bei diesem Test wird für jeden Messpunkt die Steigung auf bezogen auf den Nullpunkt bestimmt. Dabei wird untersucht, ab welchem Messpunkt die Regressionsgerade sich krümmt. Für die Kalibrierdaten wird das Polynom 2. Grades (𝑦 = 𝑐𝑥2 + 𝑏𝑥 + 𝑎) bestimmt und aus dieser Funktion wird der Koeffizient b berechnet. Dann wendet man seine intern festgelegten Toleranzen an (z.B. 10%) und berechnet damit den Schwellenwert R0. Dabei ist außerdem das Vorzeichen des quadratischen Teils der Funktion zu beachten, da dieses Auskunft über die Form der Kurve gibt. Wenn es negativ ist, handelt es sich um konkave Kalibrierkurve und R0 wäre dann 0,90 x b; bei konvexen Kurven ist es 1,10 x b. Anschließend berechnet man die Responsivität R = y/x für jeden einzelnen Messpunkt (das ist das gleiche wie die relative Response) und vergleicht sie mit dem Schwellenwert R0. Für konvexe Kalibrierkurven gilt, dass R ≤ als R0 sein sollte, sonst liegt dieser Messpunkt im gekrümmten Bereich.
Wir schauen uns das wieder am obigen Beispiel der photometrischen Nitritbestimmung an. Dieses Beispiel lässt sich durch die lineare Gleichung 𝑦 = 0,0082𝑥 - 0,0107 abbilden und das Polynom 2. Grades beträgt 𝑦 = 0,00002𝑥2 + 0,0067𝑥 + 0,0008 (zur Herleitung der quadratischen Gleichung sei auf mathematische Grundkenntnisse verwiesen). Der quadratische Teil hat ein positives Vorzeichen, also handelt es sich um eine konvexe Kurve und b ist 0,0067. Mit 1,1 (weil 10%) multipliziert ergibt sich ein Schwellenwert R0 von 0,00736:
| Nr. Kalibrierstandard | Konzentration (xi) [µg/L] | Extinktion (yi) [-] | Responsivität R = y/z [1/µg*L-1] | Vgl. mit R0 (=0,00736) |
| 1 | 0,66 | 0,0037 | 0,00561 | R < R0 |
| 2 | 1,32 | 0,0084 | 0,00636 | R < R0 |
| 3 | 2,64 | 0,0181 | 0,00686 | R < R0 |
| 4 | 5,26 | 0,0365 | 0,00694 | R < R0 |
| 5 | 6,58 | 0,0459 | 0,00698 | R < R0 |
| 6 | 7,90 | 0,0554 | 0,00701 | R < R0 |
| 7 | 10,60 | 0,0752 | 0,00709 | R < R0 |
| 8 | 26,00 | 0,1885 | 0,00725 | R < R0 |
| 9 | 44,71 | 0,3339 | 0,00747 | R > R0 |
| 10 | 63,19 | 0,4884 | 0,00773 | R > R0 |
| 11 | 82,18 | 0,6595 | 0,00803 | R > R0 |
| 12 | 100,00 | 0,8383 | 0,00838 | R > R0 |
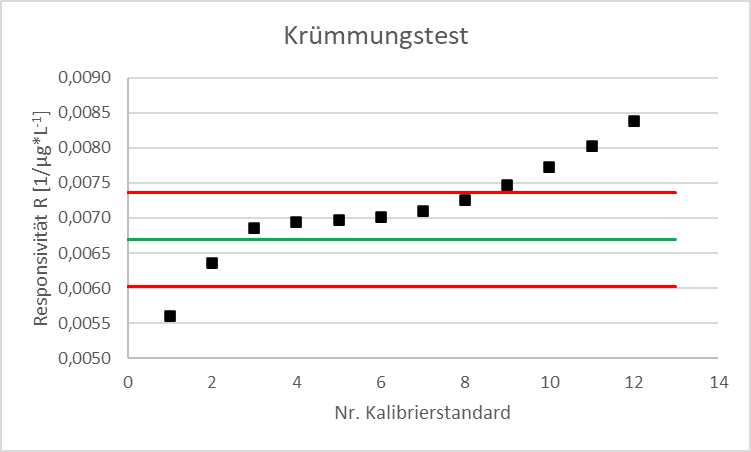
Analog zum Linearitätstest mit „Punkt-zu-Punkt-Steigung“ kommen wir auch mit diesem Linearitätstest zur gleichen Aussage 😉
Wer sich jetzt fragt, was denn mit dem 1. Kalibrierstandard ist, da der ja auch außerhalb der Toleranz liegt, dem sagt die Norm, dass dieser durch das Offset verursacht wird und wir uns im Rahmen der Kalibrierung nur für den rechten, gekrümmten Bereich (Responsivität für hohe Konzentrationen) interessieren.
Linearitätstest nach Mandel
Abschließend ein paar Worte zum Anpassungstest nach Mandel. Wenn der Arbeitsbereich nur über eine Dekade geht, Varianzenhomogenität vorliegt (wie vormals gefordert) und die Messpunkte äquidistant verteilt sind, gibt der Linearitätstest nach Mandel eine gute Auskunft, ob die lineare Kalibrierfunktion im Vergleich zur quadratischen ausreichend geeignet ist. Wenn sich die Kalibriergerade jedoch über mehrere Dekaden erstreckt und die Messpunkte auf einer logarithmischen Skala annähernd äquidistant verteilt sind, kommt man mit dem Mandel-Test sehr häufig zum Ergebnis „nicht linear“ und muss daher den Arbeitsbereich einschränken. Aus diesem Grund empfiehlt die DIN 38402-51 von 2017 inzwischen den Linearitätstest mit Punkt-zu-Punkt Steigung.
Dennoch soll der Mandel-Test hier in Kürze vorgestellt werden. Für diesen Test werden die lineare Kalibrierfunktion mit der Kalibrierfunktion 2. Grades verglichen. Dafür werden jeweils die Reststandardabweichungen bei beiden Funktionen berechnet (wie das bei einer linearen Funktion geht, ist hier im Update vom 03.11.2023 beschrieben, siehe „SDResiduen“, in diesem Beitrag jetzt als sy abgekürzt). Davon werden dann jeweils die Restvarianzen (sy lin2 bzw. sy quad2) gebildet und die Varianzendifferenz DS2 gemäß DS2 = (n-2) * sy lin2 - (n-3) * sy quad2 berechnet. Die Prüfgröße PG ergibt sich aus PG = DS2 / sy quad2. Als F-Test wird die PG anschließend mit dem F-Wert einer F-Tabelle mit einem Signifikanzniveau α = 0,01 und f1 = 1 und f2 = n-3 verglichen. Wenn die PG kleiner als der tabellierte F-Wert ist, so ist der Unterschied zwischen DS2 und der Restvarianz sy quad2 nicht signifikant und die Kalibrierfunktion kann in dem untersuchten Arbeitsbereich als linear angesehen werden.
Ohne Beachtung dessen, dass in unserem obigen Beispiel der photometrischen Nitritbestimmung der Arbeitsbereich etwas mehr als 2 Dekaden umfasst, soll anhand dieses Beispiels auch der Mandel-Test vorgestellt werden:
| Lineare Funktion |
Quadratische Funktion | |
| Funktionsgleichung | 𝑦 = 0,0082𝑥 - 0,0107 | 𝑦 = 0,00002𝑥2 + 0,0067𝑥 + 0,0008 |
| Reststandardabweichung sy | 0,0146 | 0,0019 |
| Restvarianz (sy lin2 bzw. sy quad2) | 0,0002125 | 0,0000037 |
| Varianzendifferenz DS2 | 0,00209 | |
| Prüfgröße PG | 571,8 | |
| Tabellierter F-Wert | 10,56 | |
PG ist deutlich größer als der tabellierte F-Wert, entsprechend ist unser Beispiel natürlich nicht linear, was wir ja auch schon von den vorherigen Linearitätstests wussten. Doch auch wenn wir den Arbeitsbereich auf bis zu 26 µg/L eingrenzen, ist die PG immer noch größer als der korrespondierende F-Wert. Erst bei einer Eingrenzung des Arbeitsbereichs auf 0,66 – 10,6 µg/L erhalten wir die Aussage, dass dieser Arbeitsbereich linear ist…
Zusammengefasst erscheint mir der Linearitätstest mit „Punkt-zu-Punkt-Steigung“ rechnerisch am einfachsten, da ich nicht erst die Kalibrierfunktion 2. Grades und weitere Größen bestimmen muss. Die Nachteile des Linearitätstests nach Mandel haben wir oben schon angerissen. Welcher Test aber wann am besten angewendet werden sollte, ist abhängig von der Breite des Arbeitsbereichs, der Verteilung der Messpunkte, dem persönlichen Empfinden oder internen Vorgaben.
