Wie bestimme ich die LOD mit Hilfe der Kalibrierfunktion?
Im Rahmen von Methodenvalidierungen ist es bei Reinheitstests erforderlich, die Nachweisgrenze (Limit of detection, LOD; oder auch DL = detection limit) bzw. die Bestimmungsgrenze (Limit of quantification, LOQ) zu ermitteln. Dies kann z.B. unter Anwendung der Kalibriergeraden erfolgen und wird dann in der Literatur als „Kalibriergeradenverfahren“ bezeichnet.
Am Beispiel der Nachweisgrenze werden dafür von der Validierungsguideline ICH Q2(R1) in Abschnitt 6.3 bzw. 6.3.2 folgende Vorgaben gemacht:
Zur Berechnung gilt die Formel: DL = 3,3 x σ / S. Dabei ist S die Steigung der Kalibriergerade und σ die Standardabweichung der Reaktion (response). Und genau diese Standardabweichung darf auf verschiedene Arten ermittelt werden, u.a. mit Hilfe einer Kalibriergerade:
„A specific calibration curve should be studied using samples containing an analyte in the range of DL. The residual standard deviation of a regression line or the standard deviation of y-intercepts of regression lines may be used as the standard deviation.“.
Das klingt interessant. Da uns dies in Kundenprojekten noch nicht untergekommen ist, wollte ich der Frage einmal nachgehen, wie man das eigentlich praktisch macht. Das sollte ja nicht so schwer sein, dachte ich. Doch ich wurde eines Besseren belehrt, denn an dieser Frage scheiden sich die Geister. Im Zuge der Recherche bin ich auf vielfältige Möglichkeiten gestoßen.
Eine oder ganz viele Geraden und was steckt dahinter?
In allem einig und auch von der Guideline vorgegeben ist die Tatsache, dass dafür nicht die „normale“ Kalibriergerade über den Messbereich (wie sie in der Linearitätsbestimmung ermittelt wurde) genommen werden sollte, sondern eine, die den unteren Bereich in der vermuteten Umgebung der Nachweisgrenze umfasst. Dies hat den einfachen mathematischen Hintergrund, dass bei der Verwendung der „normalen“ Kalibriergerade, welche ja deutlich höhere Werte umfasst, der Schwerpunkt der Gerade nach weiter oben verschoben ist und eine daraus ermittelte Nachweisgrenze entsprechend einen viel zu hohen Wert aufweisen würde. Daher ist es empfehlenswert, als höchste Konzentration nicht mehr als das 10fache der vermuteten Nachweisgrenze einzusetzen [1, 2].
Ok, also mit einer Gerade im Bereich des LOD. Ja, aber wirklich nur mit einer Gerade? Und mit wie vielen Konzentrationen?
Diesbezüglich existieren die unterschiedlichsten Meinungen. Mathematisch möglich wäre es mit nur einer Geraden; aber auch zwei oder mehrere Geraden oder mehrere Injektionen finden Anwendung. Bevor wir uns diese Möglichkeiten einmal an praktischen Beispielen ansehen, sollten wir jedoch erst mit dem mathematischen Hintergrund beschäftigen.
Einer Regressionsgeraden (y = mx + c) liegt die Methode der kleinsten Fehlerquadrate zu Grunde. Da nicht alle Datenpunkte zu 100% auf der Gerade liegen, bildet sie den bestmöglichen Ausgleich daraus ab. Entsprechend existiert eine ihr innewohnende Standardabweichung. Visualisiert sieht das so aus:
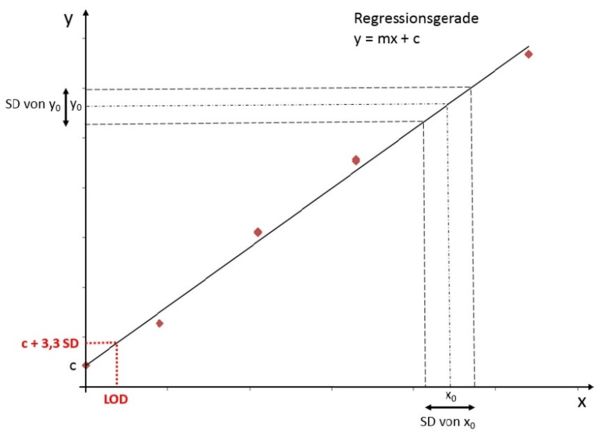
Bei dieser Abbildung möge man bitte berücksichtigen, dass die Breiten für die Standardabweichungen stark vergrößert dargestellt sind und die LOD-Darstellung daher hier nicht wirklich mit 3,3*SD übereinstimmt…
Unter Berücksichtigung der 3,3fachen Standardabweichung können wir den Y-Achsenabschnitt des LOD mit folgender Formel berechnen: yLOD = 3,3 σ + c und die LOD-Konzentration (x) mit x = (yLOD − c) / m. Kombiniert ergibt das x = 3,3 σ / m, womit wir die oben von der ICH vorgegebene Formel hergeleitet haben.
Mathematisch gesehen gelten folgende Voraussetzungen bei der Anwendung des Kalibriergeradenverfahrens [2]:
- im Bereich des vermuteten LOD ist Linearität gegeben (sonst macht das ja gar keinen Sinn)
- die Messwerte (response / signal) der Proben sind normal verteilt und voneinander unabhängig
- im Kalibrierbereich besteht Varianzenhomogenität.
Da in der Praxis diese Bedingungen nicht unbedingt zu 100% eingehalten werden (können), ist zu bedenken, dass dem ermittelten Wert eine gewisse Ungenauigkeit zu Grunde liegen kann.
Ein Praxisbeispiel zur Veranschaulichung
Schauen wir uns das Ganze nun einmal praktisch an. Dafür wurden von einem realen Beispiel ausgehend Werte für 4 Geraden mit jeweils 5 Messpunkten mit je 3 Replikaten im Bereich des vermuteten LOD konstruiert. Bei dem realen Experiment wurde ein zuvor während der Methodenentwicklung ermitteltes LOQ der RP-HPLC Methode mit dem Signal-to-Noise-Verfahren verifiziert. Dieses lag bei 6 µg/mL. Daraus wurde das vermutete LOD mit 1,8 µg/mL abgeleitet.
Die folgende Tabelle zeigt die Mittelwerte der „Messwerte“ dieser konstruierten Experimente:
| Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | |
| Konz. [µg/mL] | Area [µAU*s] | |||
| 1,8 | 25364 | 25776 | 27016 | 25566 |
| 4,2 | 68407 | 68527 | 69041 | 68568 |
| 6,6 | 108226 | 108239 | 109760 | 108342 |
| 10,8 | 173944 | 173497 | 175987 | 173747 |
| 15,0 | 235865 | 235474 | 247231 | 235686 |
Diese Messwerte wurden einer Regressionsanalyse unterzogen und die Regressionsgeraden mit Steigung m, Y-Achsenabschnitt c, Bestimmtheitsmaß R2 sowie Standardabweichung des Y-Achsenabschnitts und der Residuen bestimmt. Dafür gibt es in Excel verschiedene Möglichkeiten. Eine ist die Anwendung der RGP-Funktion, welche als etwas tricky empfunden werden kann. Eine andere ist der Weg über den Reiter „Daten“ → „Datenanalyse“ → Regression → Auswahl der zu untersuchenden Daten und Anklicken des Feldes „Residuen“→ Anklicken von „ok“, wonach ein Ausgabefenster mit einer Vielzahl statistisch interessanter Informationen erscheint. Darunter sind dann natürlich auch die Infos zur Standardabweichung der Residuen (im Feld B7) und zu der des Y-Achsenabschnittes (im Feld C17). GANZ WICHTIG: Auch wenn Excel diese Felder mit SE (= Standardfehler, standard error) ausgibt, verbirgt sich dahinter wirklich SD und NICHT SE. Ich habe das überprüft, siehe Abschnitt unten. Zur ausführlichen Erklärung dieser Funktionen seien dem geneigten Leser YouTube-Videos ans Herz gelegt ;-)
Folgende Ergebnisse wurden erhalten:
| Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | |
| Regressionsgerade | y=15878x+416 | y=15814x+849 | y=16562x-1389 | y=15844x+699 |
| R2 | 0,9987 | 0,9988 | 0,9997 | 0,9987 |
| Steigung m | 15878 | 15814 | 16562 | 15844 |
| Y-Achsenabschnitt c | 416 | 849 | -1389 | 699 |
| SDY-Achsenabschnitt | 2943 | 2849 | 1429 | 2937 |
| SDResiduen | 3443 | 3333 | 1672 | 3436 |
[Kleine Anmerkung an Rande: Interessanterweise können die so berechneten Werte für das Bestimmtheitsmaß R2 von denen in einer Abbildung angezeigten abweichen… aber ist wieder eine andere Geschichte.]
Mit den so erhaltenen Werten für die Standardabweichung des Y-Achsenabschnittes bzw. der residualen Standardabweichung kann nun gemäß der bekannten Formel LOD = 3,3 SD / m die LOD berechnet werden:
| Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | |
| LOD in µg/mL berechnet mit SDY-Achsenabschnitt | 0,61 | 0,59 | 0,28 | 0,61 |
| LOD in µg/mL berechnet mit SDResiduen | 0,72 | 0,70 | 0,33 | 0,72 |
In diesem konstruierten Beispiel weichen die Ergebnisse - abgesehen von Experiment 3 - nicht sehr stark voneinander ab. Für die Realität ist es sicherlich empfehlenswert, mehr als nur eine Gerade auszuwerten (ob es 4 sein müssen, sei mal dahingestellt) und bestenfalls die Experimente auf verschiedene Tage und Tester aufzuteilen, um wirklich unabhängige Ergebnisse zu generieren. Inwiefern dieser Aufwand gerechtfertigt ist, bleibt jedem selbst überlassen.
Interessant ist bei der Betrachtung der Ergebnisse auch die Feststellung, dass diese mit einem Mittelwert von 0,66 µg/mL (unter Ausschluss von Experiment 3) etwas niedriger sind als das eingangs vermutete LOD mit 1,8 µg/mL. Dies mag aber bereits daran liegen, dass zur Bestimmung der LOQ ein anderes Bestimmungsverfahren herangezogen wurde (siehe auch nächster Abschnitt).
Die im Beispiel angewandte Anzahl an Geraden und Messpunkten erhebt keineswegs den Anspruch darauf, dass eine LOD-Bestimmung genauso gemacht werden müsse. Ganz im Gegenteil, sie soll als Diskussionsstartpunkt fungieren, da mir im Zuge der Recherche auch andere Möglichkeiten begegnet sind. So sind z.B. auch 2 Geraden (eine oberhalb und eine unterhalb des vermuteten LODs) eine interessante Option und im Guidance-Dokument für die LOD- und LOQ-Bestimmung von Verunreinigungen in Futter- und Nahrungsmitteln wird zudem eine andere Berechnung für die dort aufgeführte Vorgehensweise angewandt [2]. Natürlich ist ein solches Dokument nicht für Arzneimittel verbindlich, kann aber möglicherweise ebenfalls eine Option zur Orientierung darstellen.
Unterschiedliche Bestimmungsverfahren führen zu verschiedenen Ergebnissen
Ein kurzer Blick in zwei Publikationen [3, 4] zeigt, dass sich die Ergebnisse unterscheiden, je nachdem welches Verfahren zur Bestimmung von LOD und LOQ (visuelle Prüfung, Signal-to-Noise oder das in diesem Blogbeitrag beschriebene Kalibriergeradenverfahren) angewandt wird. Selbst innerhalb des Kalibriergeradenverfahrens können recht unterschiedliche Ergebnisse erhalten werden, je nachdem ob die Standardabweichung des Y-Achsenabschnitts oder die der Residuen der zu Grunde liegenden Regressionsgerade verwendet wird.
Aus regulatorischer Sicht ist keine Begründung für das angewandte Bestimmungsverfahren notwendig. Vom wissenschaftlichen Standpunkt erachte ich das als fragwürdig.
Was sind Eure Erfahrungen und was ist Euer Standpunkt?
Update 03.11.2023: Verwendung von SD oder SE?
Bei diesem Artikel habe ich immer mal wieder Anfragen erhalten, was denn jetzt für die Berechnung der LOD mittels Kalibriergeradenverfahrens verwendet werden sollte: SE oder SD? Dazu herrscht Einiges an Unklarheit, was sicherlich auch an der wie oben bereits erwähnten falschen Bezeichnung von SE für SD in Excel liegen mag. Entsprechend finden sich auch viele Diskussionen zum Thema SE vs. SD zur Berechnung des LOD.
Sehr schön sind jedoch die Erläuterungen zu diesem Thema in [5]. Mit Hilfe der dortigen Ausführungen habe ich exemplarisch den Rechenweg für meine obige Gerade aus Experiment 1 verifiziert. Dazu berechne ich mir einige Hilfsgrößen, wie in nachfolgender Tabelle gezeigt:
| Conc. (xi) |
Response (yi) |
(xi-X̅) | (xi-X̅)2 |
ŷi |
(yi-ŷi) | (yi-ŷi)2 |
xi2 | ||
| 1,8 | 25364 | -5,9 | 34,6 | 28997 | -3633 | 13197214 | 3,2 | ||
| 4,2 | 68407 | -3,5 | 12,1 | 67105 | 1302 | 1695469 | 17,6 | ||
| 6,6 | 108226 | -1,1 | 1,2 | 105213 | 3013 | 9080934 | 43,6 | ||
| 10,8 | 173944 | 3,1 | 9,7 | 171902 | 2042 | 4170512 | 116,6 | ||
| 15 | 235865 | 7,3 | 53,6 | 238590 | -2725 | 7425333 | 225,0 | ||
| n = 5 | |||||||||
| Mean (X̅) | 7,7 | - | Sum | - | 111,2 | - | - | 35569461 | 406,1 |
Die ersten beiden Spalten „Conc.“ und „Response“ entstammen der allerersten Tabelle dieses Beitrags. Für die Konzentrationen berechne ich den Mittelwert X̅. Diesen subtrahiere ich von jedem Einzelwert (xi-X̅). Die so erhaltenen Werte werden quadriert ((xi-X̅)2) und aufsummiert (∑(xi-X̅)2, hier: 111,2). Um ŷi (das sind die theoretischen Werte) ausrechnen zu können, muss ich mir erst die Steigung meiner Regressionsgeraden (15878) und deren Y-Achsenschnittpunkt (416) berechnen. Anschließend kann ich durch Einsetzen der jeweiligen xi-Werte in die Geradengleichung (y = 15878*x + 416) die korrespondierenden theoretischen ŷi-Werte ermitteln. Nun kann ich durch Subtraktion von ŷi von yi die Residuen berechnen (yi-ŷi), um diese anschließend zu quadrieren ((yi-ŷi)2). Die Summe davon ist die RSS (residual sum of squares, hier: 35569461). Außerdem brauchen wir noch die Summe der quadrierten xi-Werte (∑xi2, hier: 406,1).
Mit folgenden Formeln kann ich schließlich SDResiduen und SDY-Achsenabschnitt berechnen:
SDResiduen = √(RSS/(n-2)) = √(35569461/3) = 3443
SDY-Achsenabschnitt = SDResiduen * √((∑xi2 / (n * ∑(xi-X̅)2))) = 3443 * √((406,1 / (5 * 111,2))) = 2943
Und siehe da, das sind genau die Werte, die Excel oben bei der Regressionsanalyse fälschlicherweise als SEs ausgegeben hat…
Bei einer sehr interessanten Diskussion zum Thema SE vs. SD zur LOD-Berechnung mittels Kalibriergerade bei ResearchGate bin ich übrigens auch auf Folgendes gestoßen: SD gibt Auskunft über die Streuung innerhalb einer (kleinen) Stichprobe (n), während sich SE auf die Variabilität innerhalb der Grundgesamtheit / Population (N) bezieht. Ein entsprechender, mir sehr einleuchtender Vorschlag war daher, SD am Anfang / während der Methodenentwicklung zu verwenden, wenn nur eine kleine Stichprobe vorliegt und die Informationsbasis noch nicht so genau ist und SE später zu verwenden, wenn die Methode bereits vollständig entwickelt wurde und ein größerer Datensatz vorliegt. Da SE niedriger als SD ist, stellt die Verwendung von SD für die Berechnung von LOD zu Projektbeginn einen konservativen Ansatz dar, da entsprechend höhere Werte erhalten werden. Für die spätere Routine kann dann anschließend die Verwendung von SE (basierend auf einem größeren Datensatz) eine bessere Abschätzung für LOD liefern.
Wir sollten dabei jedoch im Hinterkopf behalten, dass generell ein auf diese Weise berechnetes LOD grundsätzlich nur einen groben Schätzwert darstellt und experimentell mit Hilfe von nahe der berechneten Konzentration eingestellten Proben überprüft werden sollte, wie dies ja auch die ICH Q2(R1) fordert.
Referenzen
[1] Kromidas S. (2011). Validierung in der Analytik, Wiley-VCH Verlag GmbH & Co KGaA, Weinheim, ISBN 978-3-527-32939-7
[2] Robouch P., Stroka J., Haedrich J., Schaechtele A., Wenzl T. (2016). Guidance document on the estimation of LOD and LOQ for measurements in the field of contaminants in feed and food
[3] Saadati N., Abdullah M.P., Zakaria Z., Sany S.B., Rezayi M., Hassonizadeh H. (2013). Limit of detection and limit of quantification development procedures for organochlorine pesticides analysis in water and sediment matrices, Chem Cent J., Vol. 7(1):63
[4] Şengül Ü. (2016). Comparing determination methods of detection and quantification limits for aflatoxin analysis in hazelnut. J Food Drug Anal., Vol. 24(1):56-62.
[5] Ellison S.R.L., Barwick V.J., Duguid Farrant T.J. (2009, 2nd edition). Practical Statistics for the Analytical Scientist: A Bench Guide, RSC Publishing, Cambridge, ISBN 978-0-85404-131-2
P.S.: Die hier exemplarisch für die Nachweisgrenze LOD beschriebene Abhandlung lässt sich natürlich unter Anwendung der entsprechenden Formel auch auf die Bestimmungsgrenze LOQ übertragen.
