Einsatz der „relative response“ bei Methodenvalidierungen und Routinemessungen
Im pharmazeutischen Labor der Qualitätskontrolle kommen die unterschiedlichsten Analysemethoden zum Einsatz. Neben Methoden zum Nachweis der Identität des Wirkstoffs und qualitativen Untersuchungen gehören auch quantitative Bestimmungen dazu. Dabei wird ein (Kalibrier-) Standard in verschiedenen Konzentrationen bei der Analyse mitgeführt und anschließend die Intensität des Messsignals gegen die Konzentration aufgetragen.
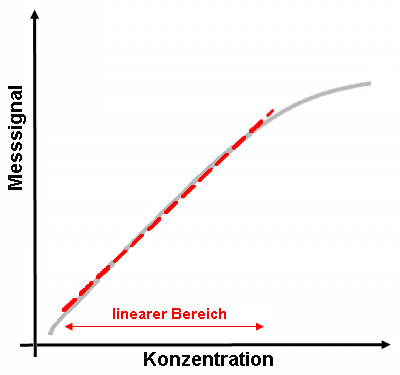
Der lineare Bereich einer solchen Standardkurve dient dann später dazu, die unbekannte Konzentration in einer Probe anhand ihres Messsignals mit Hilfe linearer Regression zu bestimmen.
Und was ist nun die “relative response”?
Wir wissen, dass ein linearer Zusammenhang anhand des Korrelationskoeffizienten R bzw. des Bestimmtheitsmaßes R2 charakterisiert werden kann, wobei ein Wert von > 0,99 eigentlich für einen sehr, sehr guten linearen Zusammenhang zwischen Messsignal und Konzentration spricht… Eigentlich… Das sagt uns nur, dass sich die Regressionsgerade sehr gut durch unsere Messwerte abbilden lässt, erzählt uns aber nichts darüber, wie weit einzelnen Messsignale doch von der idealen Linie abweichen.
Schauen wir uns doch dafür mal ein praktisches Beispiel an. Wir haben eine photometrische Methode zur Gehaltsbestimmung, bei der 4 Konzentrationen des Standards und der Blank-Wert in Triplikaten gemessen wurden:
| Konz. [µg/mL] |
Absorption [-] | |||
| Replikat 1 | Replikat 2 | Replikat 3 | Mittelwert | |
| Blank (0) | 0,020 | 0,020 | 0,018 | 0,019 |
| 2 | 0,073 | 0,073 | 0,102 | 0,083 |
| 4 | 0,129 | 0,130 | 0,130 | 0,130 |
| 6 | 0,165 | 0,169 | 0,171 | 0,168 |
| 8 | 0,256 | 0,258 | 0,258 | 0,257 |
Die Mittelwerte abzüglich des Blanks werden gegen die Konzentrationen aufgetragen und wir erhalten folgende Standardkurve:
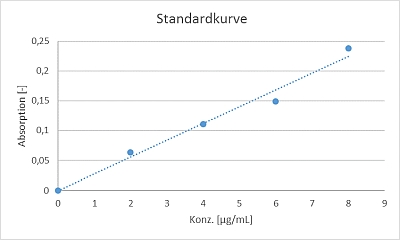
Auf den ersten Blick sieht diese doch gar nicht so übel aus und auch der berechnete Korrelationskoeffizient ist mit 0,9904 verdammt gut. Also alles im grünen Bereich? Nicht so ganz, es liegen ja nicht alle Messwerte so ganz auf der Gerade, sondern weichen ein klein wenig nach oben bzw. unten ab. Um das besser beurteilen zu können, ermitteln wir jetzt die „relative response“. Dahinter verbirgt sich nichts anderes als die Division des Messsignals durch die Konzentration (bitte nicht mit der Steigung der Kalibriergerade / „calibration sensitivity“ verwechseln, da Steigung = Δy/Δx). Das machen wir für jede der 4 Konzentrationen und berechnen dann auch noch den Mittelwert daraus, sowie entsprechende Grenzwerte (hier: ± 10% vom Mittelwert, diese Grenzwerte können z.B. auf der Messunsicherheit der verwendeten Geräte oder internen Genauigkeitsanforderungen basieren):
| Konz. [µg/mL] | Messsignal (abzüglich Blank) [-] | Relative response [-] | Relative response Mittelwert [-] | Relative response Grenzen (Mittelwert ± 10%) | Individuelle relative response innerhalb der Grenzen? |
| 2 | 0,063 | 0,032 | 0,028 | 0,026 - 0,031 | nein |
| 4 | 0,110 | 0,028 | ja | ||
| 6 | 0,149 | 0,025 | nein | ||
| 8 | 0,238 | 0,030 | ja |
Wir erwarten, dass die ermittelten individuellen relativen Response Werte um die horizontale Mittelwertlinie herum schwanken, im Idealfall sollten sie alle auf dieser Linie liegen oder zumindest nicht allzu stark davon abweichen. Um uns das besser vorzustellen, tragen wir jetzt analog einer Qualitätsregelkarte die ermittelten individuellen relativen Response Werte gegen die Konzentration auf, zeichnen den Mittelwert als grüne Linie und die ± 10% vom Mittelwert als äußere rote Grenzlinien ein und stellen leider fest, dass das relative Messsignal bei den Konzentrationen 2 und 6 µg/mL knapp außerhalb der von uns gewählten Grenzen liegt. Damit wäre trotz eines Korrelationskoeffizienten von > 0,99 keine Linearität gegeben.
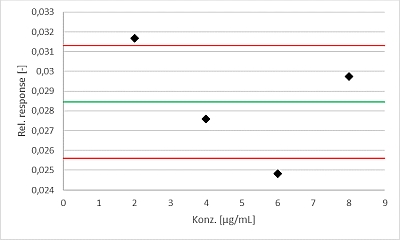
Die Darstellung erinnert ein wenig an einen Residuenplot (Residuendiagramm), welches vom Grundgedanken ja auch nichts Anderes aussagen möchte. Mir persönlich erscheint jedoch die Berechnung des relativen Messsignals etwas einfacher als die der Residuen, aber das mag Geschmackssache sein…
(Wir sehen in unserem Beispiel auch noch, dass das 3. Replikat der 2 µg/mL Konzentration überhaupt nicht passt, aber das ist wieder eine andere Geschichte…)
Und was bringt uns das jetzt – wann kann man das anwenden?
Die Frage ist berechtigt. Da fallen mir spontan zwei Möglichkeiten ein.
Erstens ist eine Anwendung im Rahmen von Methodenvalidierungen bei Untersuchungen zur Linearität gegeben, denn die Richtlinie zur Methodenvalidierung, die ICH Q2(R1), fordert Folgendes: „[…] In addition, an analysis of the deviation of the actual data points from the regression line may also be helpful for evaluating linearity.“. Mit der Berechnung der relativen Response und einem entsprechenden Akzeptanzkriterium (wie z.B., dass die Einzelwerte nicht mehr als ± 10% vom Mittelwert abweichen dürfen, wie in unserem Beispiel) wird dieser Forderung Rechnung getragen. Weitere statistische Möglichkeiten einer Untersuchung der Einzelwerte wären Hat Values und Cook’s Distance…
Und zweitens kann die Berechnung der relativen Response des Standards unter Anwendung entsprechender Grenzwerte auch als Systemeignungstest (SST) bei nicht ganz so super-robusten Methoden, die gerne mal zu Ausreißern neigen, bei den Routinemessungen im Rahmen der Freigabe- und Stabilitätsanalytik angewendet werden.
