Lineare versus nicht-lineare Regression: Was ist zu beachten?
In jeder Methode, bei der es um die Quantifizierung eines Analyten eines Arzneimittels oder dessen Wirkstoffs geht, ist die Linearität einer Kalibriergeraden ein ausschlaggebendes Kriterium für die Richtigkeit der Werte. Die gemessenen Werte sollten im besten Fall also direkt proportional zur eingesetzten Konzentration darstellbar sein. Die meisten Messmethoden haben ihre Grenzen, weshalb man den messbaren Bereich (linearen Bereich) oft eingrenzt.
Laut ICH Q2(R2) Leitfaden zur Methodenvalidierung ist die Response (Linearität) im berichtspflichtigen Arbeitsbereich (reportable range) mit der Methode der kleinsten Quadrate nachzuweisen. Unbedingt zu vermeiden ist es, den erzeugten Daten eine lineare Regression aufzuzwingen, wo unter Umständen keine vorhanden ist. Lässt sich bei Auftragung der Konzentration gegen die Messwerte eine Kurve erahnen, sollte eine genauere Regressionsanalyse in Betracht gezogen werden.
Linear oder nicht-linear: Korrelationskoeffizienten geben Auskunft
Ist eine sehr seichte Kurve erkennbar, liegt die Entscheidung, ob eine lineare Regression ohne Bedenken angewendet werden kann, im Auge des Betrachters. Eine Hilfe kann hier die Berechnung zweier Korrelationskoeffizienten (R) sein. Der Pearson-Korrelationskoeffizient betrachtet nur lineare Zusammenhänge. Ist er beispielsweise deutlich kleiner als 0,95, kann es sich entweder um eine zu breite Streuung der Messergebnisse oder um eine nicht-lineare Korrelation handeln. Gewissheit kann man durch den sogenannten Spearman-Korrelationskoeffizienten erlangen. Dieser beachtet sowohl lineare als auch nicht-lineare Korrelationen. Berechnet man beide Koeffizienten und erhält für den Spearman-Koeffizienten einen deutlich höheren Wert als für den Pearson-Koeffizienten, so handelt es sich aller Wahrscheinlichkeit nach um eine nicht-lineare Korrelation. Sind beide Korrelationskoeffizienten nahezu identisch, ist es eine lineare Korrelation.
Transformation der Rohdaten
Bei einer nicht-linearen Abhängigkeit schlägt der ICH Q2(R2) Leitfaden eine mathematische Transformation der Rohdaten vor, um eine geeignete lineare Regression zu schaffen. Doch wie macht man das am besten?
In unserem Beispiel haben wir fiktive Werte generiert, die einer polynomischen Funktion zweiten Grades folgen (y = ax2 + bx + c). Die grafische Darstellung ist in der ersten Abbildung (blaue Werte) zu sehen.
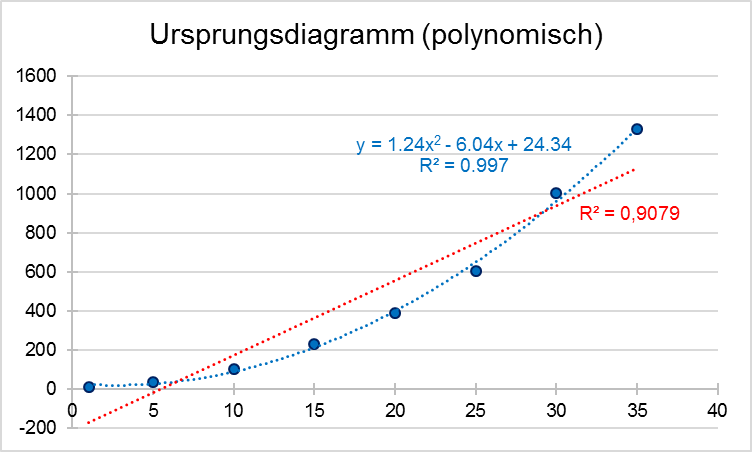
Hier wird deutlich, dass guten Gewissens keine lineare Regression anwendbar ist. Probiert man es dennoch, bekommt man ein Bestimmtheitsmaß (R2) von 0,908. Eine polynomische Funktion lässt sich hingegen sehr gut hineinlegen (blaue Linie). Eine einfache und gut anzuwendende Methode, die polynomische Funktion in eine lineare Abhängigkeit zu bringen, beschreibt die sogenannte „Potenzleiter“. Je nach Art der Kurvenkrümmung kann man anhand der Potenzleiter die Veränderungen bestimmen, die man an den x- bzw. y-Variablen vornehmen muss, um sich einer linearen Abhängigkeit zu nähern (siehe nachfolgende Abbildung):
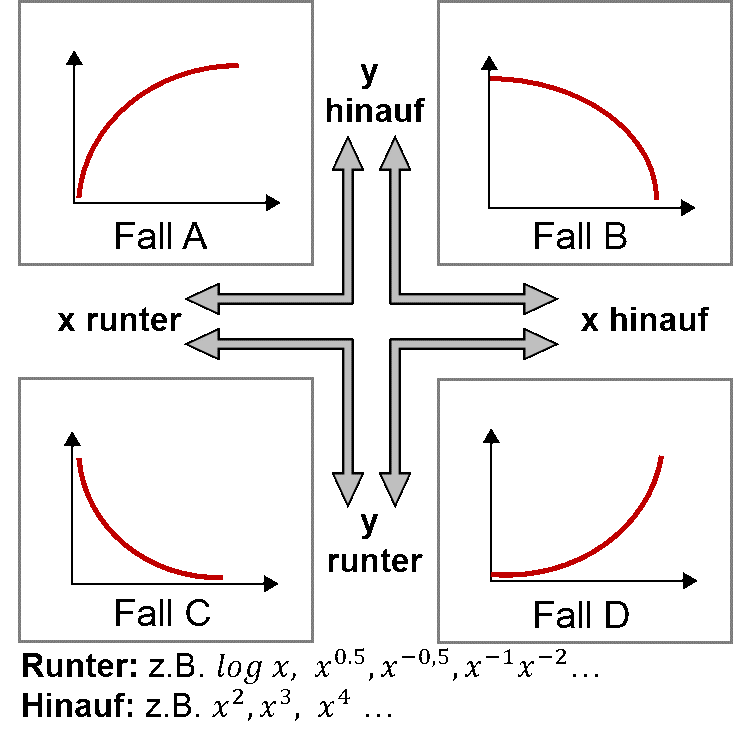
Liegt wie in unserem Beispiel eine ansteigende Kurve (also „Fall D“ der obigen Abbildung) vor, kann man die x-Variable hinauf potenzieren, indem man die Werte quadriert oder hoch 3 nimmt. Ein anderer Ansatz wäre, die y-Variable beispielsweise durch eine Logarithmusfunktion oder Wurzel herunter zu potenzieren. So kann man sich nach und nach an eine Linearität herantasten. In unserem Beispiel haben wir uns für die Anwendung der Wurzelfunktion auf die y-Variablen entschieden (= y0,5) und kommen zu folgendem Ergebnis:
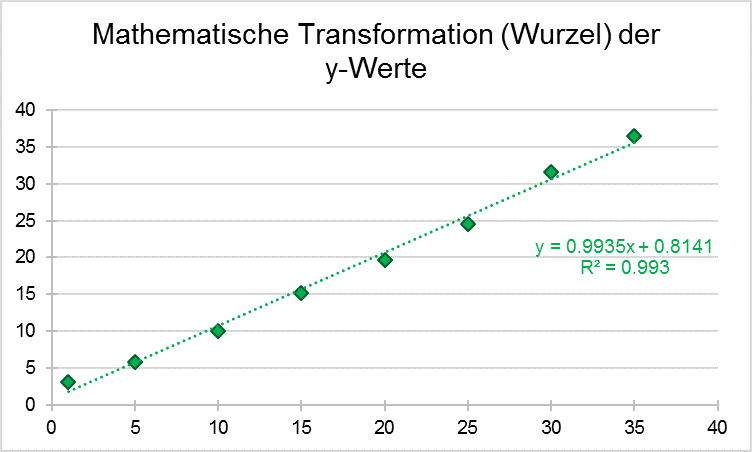
Nachdem die entsprechenden mathematischen Transformationen durchgeführt wurden, kann mit den neu erlangten x- und y-Werten die lineare Regression angewendet und das Bestimmtheitsmaß (R2) berechnet werden. In unserem Beispiel kommen wir so auf ein gutes lineares Verhältnis mit einem Bestimmtheitsmaß von 0,993. Neue Messwerte, die anhand der transformierten linearen Regression analysiert werden sollen, müssen vor ihrer Analyse derselben mathematischen Transformation unterworfen werden. In unserem Fall müssen von allen neu gemessenen y-Werten die Wurzeln gezogen werden. Anschließend können sie wie üblich anhand der Regressionsgleichung eingesetzt und nach x aufgelöst werden.
