From everyday laboratory work: Systematic and random errors
Everyone who works in a laboratory every day, be it in a pharmaceutical QC lab or a contract laboratory, will at some point deal with the following questions: “What influences good measurements? When are we able to trust our measurements?” The answer is simple: ideally no or just small random and systematic measurement errors, since measurement results are never free of errors. What’s behind, we’d like to explain a little bit in this blog article.
What does affect my measurement result?
As we can see from the illustration below, the difference between my measurement result xi and the real "true value" xRef is always based on both types of error, i.e. one part of random errors, which is seen by the degree of scatter (expressed as standard deviation, SD) of the measurement results, and another part of systematic errors.
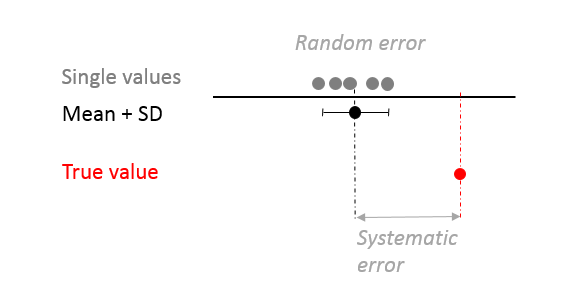
The underlying causes of such errors are diverse and encompass external influences (such as temperature), the process and the measurement device itself as well as the laboratory technician who carries out the method. Classically, systematic and random errors are distinguished.
Systematic errors
Systematic errors, also known as bias or offset, are the cause for the deviation of the mean of a series of measurements from the true value or the value considered as being correct. Thus, they influence the trueness. They are reproducible, i.e. within a series of measurements and also when repeating a measurement, a systematic error always occurs in the same extent and with the same algebraic sign. In other words, each time a measurement is carried out, they are expressed by the same shift of all measurement values.
Since systematic errors always falsify the result in the same direction, they cannot be detected by repeated measurements, i.e. a larger sample size. Only a comparison with a different second measurement method or round robin tests allow their discovery.
In contrast to random errors (explained below), the causes of systematic errors can be identified by a thorough error analysis with a close look at the measurement device used and the entire process. They are - as the name suggests - system based errors. They are caused by uncontrollable external influences, the imperfection of the measurement device or personal preferences and idiosyncrasies of the measuring person. Some typical examples are:
- An incorrectly calibrated or adjusted measurement device
- Aging of sensors
- No zero point adjustment before net weight
- Zero offset / drift
- Rounding errors in the calculation
- In case of non-constant ambient conditions, influence of the temperature regarding the measurement device or volumetric flasks (--> incorrect volume) or to the standard (--> changed density)
- Influence of magnetic fields on the measuring device
- Contaminated samples
- Instability of the sample during sampling and analysis
- No equal treatment of sample and calibration standard
- Interference of the sample matrix (overlay of a signal for another substance of the matrix on the actual measurement signal of the analyte)
Random errors
Random or statistical errors are caused by spontaneously occurring, unpredictable processes during a series of measurements and their cause can’t be determined afterwards. They are based on changes that cannot be recorded. They are characteristic for a single measurement point, this is why they vary in size and sign. Random errors are expressed by the scatter of the measurement values around the mean and thus influence the precision of the series of measurements. They can be reduced by increasing the sample size. A typical example is the device-specific background noise or in case of non-regulated / non-controlled ambient conditions a sensor drift of the device on hot days (if it has no temperature compensation built in)... but also tiny differences in the added volume of reagent, inaccuracies in visual reading or very slightly varying incubation times between the individual samples can be causes of random errors.
To get back to the beginning, we can summarize that it is useful to know the extent of systematic and random errors. That is why it makes sense to check the parameters trueness and precision during method development as part of a method qualification. It enables us to judge our measurement results. We can consider whether we can live with the identified systematic and random errors or whether a reduction of these is necessary, which would result in method optimization. A reduction of systematic errors would result in a better representation of the reality by the measurement results due to the reduction of the distance from the reference value. Knowing the presence of minor random errors enables an estimate of how many measurements are finally required to get as close as possible to the correct value.
