Von kleinen Werten mit grossem Einfluss - Sum Of Squares - Teil 2
Im ersten Teil dieses Blogartikels haben wir die RSS kennengelernt und begonnen, uns dem Einfluss der Einzelwerte zu nähern. Daran schließt dieser Teil an.
Hat Values und Cooks Distance – was beeinflusst die lineare Regression tatsächlich?
Der Einfluss eines einzelnen Datenpunktes lässt sich erst damit bestimmen, wenn man untersucht, ob das Entfernen des Datenpunktes die Regressionsgerade stark verschieben würde. Es ist durchaus möglich, dass Datenpunkte mit großem Anteil der RSS die Regressionsgerade kaum verschieben würden, wenn sie entfernt würden. Dies ist abhängig davon, in welcher Entfernung sich der Datenpunkt zu dem Rest aller anderen Datenpunkte befindet. Folgende Grafik zeigt den jeweiligen Einfluss der Datenpunkte auf die Regressionsgerade, würde man diese entfernen:
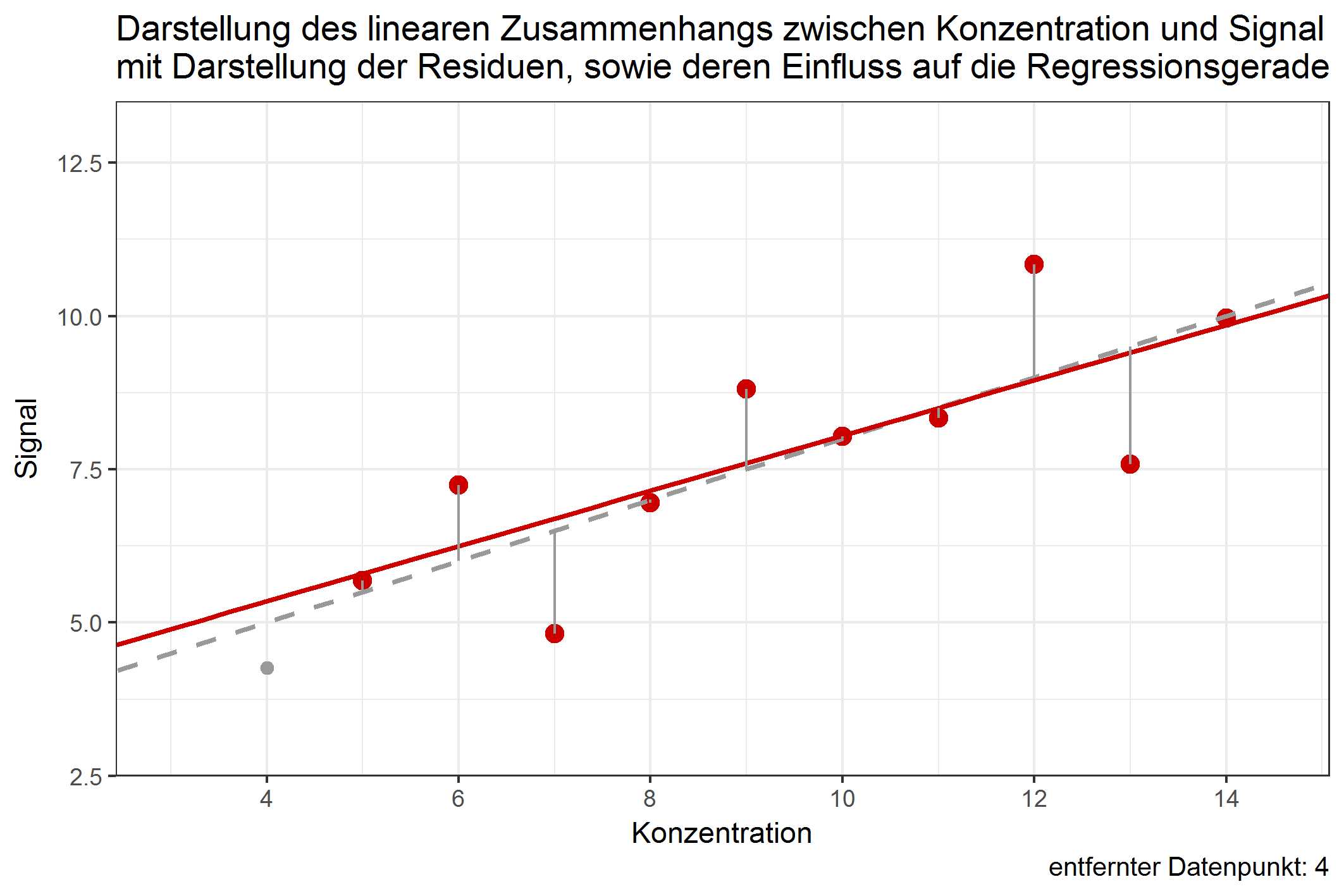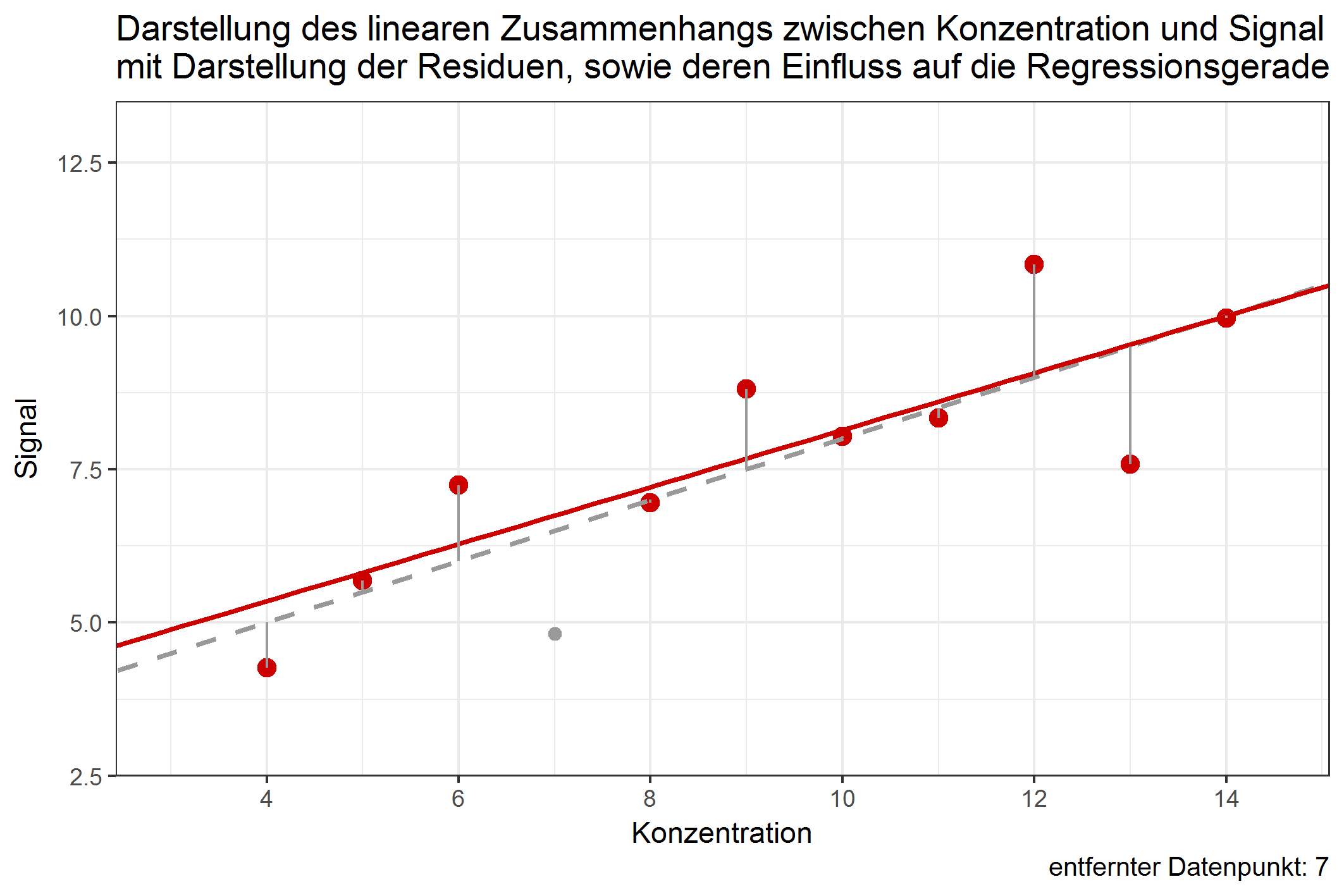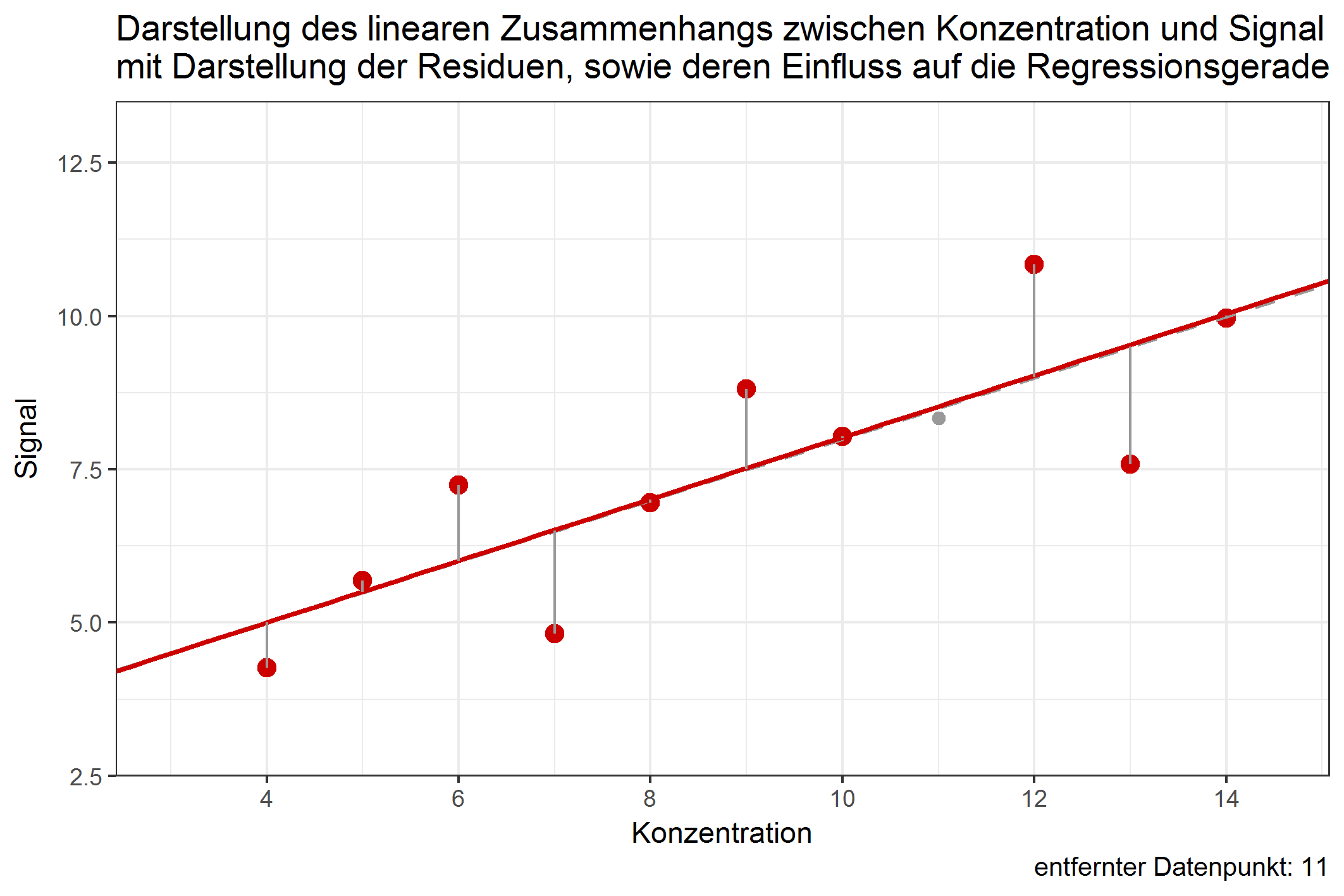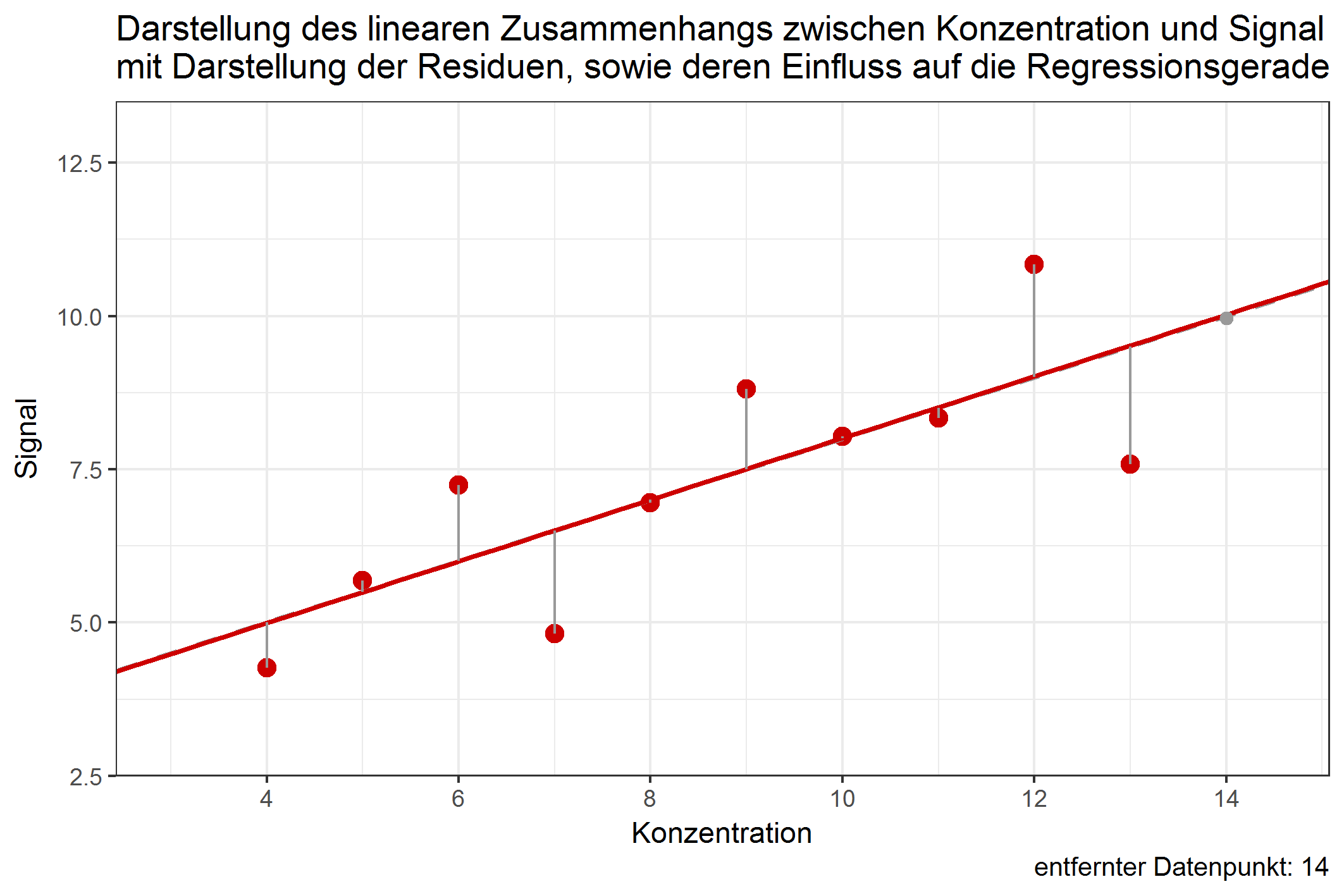
Abbildung 1: Verschiebung der Regressionsgeraden durch Weglassen einzelner Datenpunkte [ist animiert, dauert etwas - bitte länger betrachten ;-) ]
Obwohl der Wert 9 einen Anteil von über 12% an den residual sum of squares besitzt, würde ein Weglassen dieses Wertes die Gerade kaum verschieben. Im Gegenzug dazu würde das Weglassen von Datenpunkt 4 die Gerade ähnlich stark beeinflussen, obwohl dessen Anteil an der RSS nur knapp 4% beträgt. Dies ist ein Beispiel dafür, dass Werte, die (in Bezug auf die Konzentration) in größerer Entfernung zu allen anderen Punkten liegen, einen potentiell größeren Einfluss auf die Verschiebung der Regressionsgeraden haben können. Diesen Einfluss nennt man leverage. Datenpunkte mit großem leverage werden als high-leverage points bezeichnet. Das deutsche Äquivalent zu leverage lässt sich z.B. mit dem Wort „aushebeln“ beschreiben – high-leverage points sind in der Lage, die Regressionsgerade auszuhebeln, beziehungsweise deren Lage stark zu ändern. Datenpunkte an den Randbereichen der X-Werte sind dazu stärker in der Lage, als Datenpunkte, die nahe dem Zentrum der Datenpunkte liegen. In der Methodenvalidierung betrifft das vornehmlich Datenpunkte an der Bestimmungsgrenze, welche einen hohen leverage aufweisen können. Doch gerade von Werten in diesem Konzentrationsbereich muss eine hohe Richtigkeit erwartet werden. Umso wichtiger ist es, den Einfluss dieser Punkte genauestens zu untersuchen.
Die Grenze, ab der man einen high-leverage point kennzeichnet, liegt in diesem Beispiel bei 2 * (2/n) = 0,363, wobei n = 11 die Anzahl der Datenpunkte beschreibt. In Abbildung 2 sind die Datenpunkte in Bezug auf deren leverage gekennzeichnet. Synonyme für leverage sind die sogenannten hat values, oder H Werte.
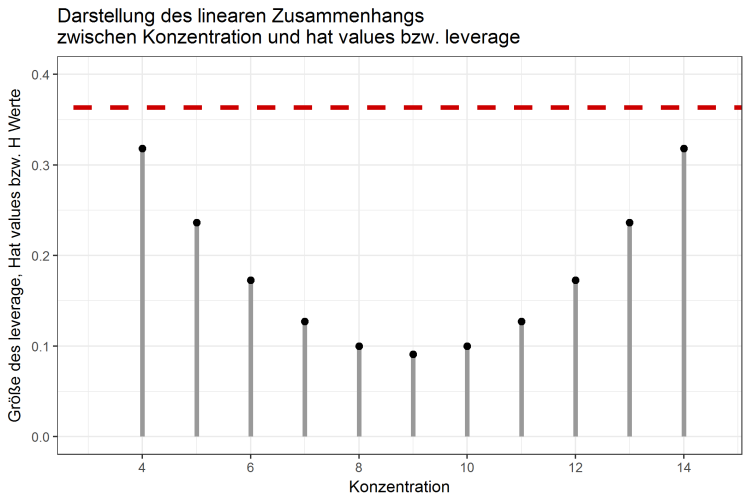
Abbildung 2: Leverage der Einzeldatenpunkte in Bezug auf die Grenze von 0,363
Die Punkte für Konzentrationen von 4, 5 als auch 13 und 14 haben hohe leverage Werte, da sie, in Bezug auf alle anderen Datenpunkte, relativ weit entfernt sind. Die leverage Werte liegen jedoch unter der Grenze von 0,363, so dass in diesem Datensatz keine high-leverage points vorhanden sind. Hohe leverage Werte sind nicht automatisch Datenpunkte mit großem Einfluss, da sie nur abhängig von der X-Koordinate (bzw. der Konzentration) sind. Die Y-Werte, also in diesem Falle die Signalintensität, spielen für die Berechnung des leverage keine Rolle. Daher kann es ebenso vorkommen, dass Datenpunkte mit geringen leverage-Werten dennoch einen starken Einfluss auf die Regressionsgerade haben und damit die Qualität der Methode besonders stark beeinflussen. Um diese Punkte zu identifizieren, benötigt man ein weiteres Maß, welches den Fokus auf die Y-Koordinaten der Daten legt.
Begutachtet man sowohl den Einfluss der X- und Y-Koordinaten jedes Einzelwertes auf die Regressionsgerade, ist es möglich, sogenannte influencial observations, also einflussreiche Datenpunkte, auszumachen. Ein solches Maß für den tatsächlichen Einfluss ist die sogenannte Cooks Distance oder die sogenannten D Werte [1]. Diese sollten ebenfalls möglichst gering sein, und sollten den Wert von, in diesem Falle, 4 / (n - 2) nicht überschreiten, wobei n die Anzahl der Datenpunkte beschreibt. In Abbildung 3 sind die Datenpunkte nach Cooks Distance aufgetragen. Der Grenzwert für diesen Datensatz hier liegt bei 4 / 9 = 0,445. In diesem Beispiel wird der Datenpunkt mit x = 13 als influencial observation gekennzeichnet, da er die Regressionsgerade besonders stark zu sich verschiebt – und dass, obwohl er nicht den größten leverage aufweist.
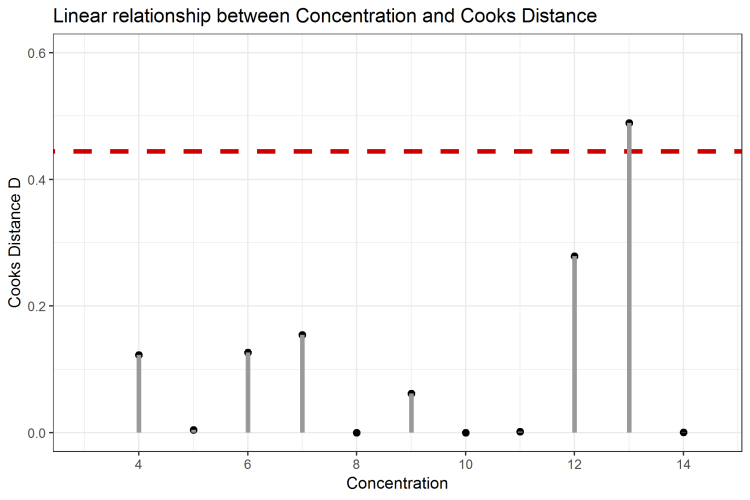
Abbildung 3: Cooks Distance zur Identifizierung von influencial observations
Die Werte von Cooks Distance sind eine “Mischung“ aus den jeweiligen Anteilen der RSS und den leverage Werten. Damit kombinieren sie die Eigenschaften aller Einzelwerte: Sie untersuchen zum einen die Abweichung jedes Wertes in Y-Koordinaten (also des Signals, der RSS), als auch die Abweichung in X-Koordinaten (also Analytenkonzentration, bzw. leverage) in Bezug auf alle anderen Punkte. Erst damit lässt sich bestimmen, wie groß der Einfluss jedes Einzelwertes auf die Regressionsgerade, und damit auf die Güte des linearen Zusammenhanges, tatsächlich ist. Eine Grafik, in der die Daten, zusammen mit Cooks Distance, beschrieben sind, könnte folgendermaßen aussehen: Die Daten und die Regressionsgerade, werden wie bisher dargestellt, und die Farbe der Datenpunkte gibt an, ob die Cooks Distance jedes Punktes den Wert von 0,445 übersteigt. Damit werden automatisch alle einflussreichen Datenpunkte gekennzeichnet.
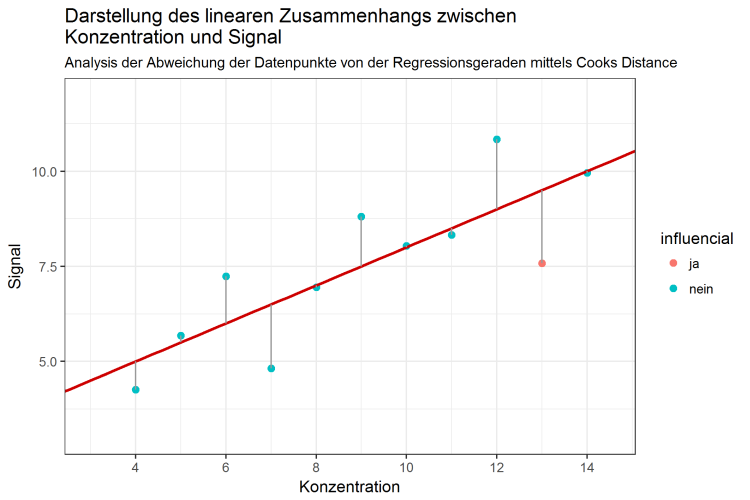
Abbildung 4: Lineare Regression und mittels Cooks Distance identifizierter einflussreicher Datenpunkt
Was ist also zu tun bei der Untersuchung der Linearität?
Die von der ICH Q2(R1) geforderte „analysis of the deviation of the actual data points from the regression line“ kann aus gutem Grund nicht nur in der visuellen Begutachtung der Datenpunkte liegen. Das Berechnen des Einflusses jedes Datenpunktes offenbart die eigentliche Qualität der linearen Regression. Die Angaben der Merkmale wie r oder R2, Anstieg und Achsenschnittpunkt, oder der RSS zeigen nur eine Hälfte der Medaille. Doch da weder die residual sum of squares, noch der R2 oder die Eigenschaften der Regressionsgeraden Hinweise auf den Einfluss von Einzelwerten geben können, sollte die „Analysis der Abweichung der eigentlichen Datenpunkte von der Regressionsgerade“ immer durchgeführt werden.
Datenpunkte mit großem Einfluss auf die Regressionsgerade können ein Indiz dafür sein, dass der lineare Zusammenhang über die gesamte Breite des Konzentrationsbereiches nicht überall gleich „gut“ sein könnte, so wie es die ICH Q2(R1) fordert. Hinweise darauf finden sich häufig nicht durch visuelle Inspektion der Daten, sondern durch Analysen wie der Berechnung der Cooks Distance. Findet man jedoch potentielle influencial observations, muss in solchen Fällen anschließend überprüft werden, in welchen Konzentrationsbereichen diese Abweichungen auftreten und ob diese Abweichungen „normal“ sind. Gegebenenfalls muss geklärt werden, mit welchen Maßnahmen diese Schwankungen zu kontrollieren und zu minimieren sind.
Fazit
Die residual sum of squares sind ein statistischer Wert, der z.B. bei der linearen Regression Anwendung findet. Seine Bedeutung wird oft vernachlässigt, gleichzeitig kann er bei falscher Interpretation für Missverständnisse sorgen. So wie der Mittelwert die Eigenschaften vieler Datenpunkte auf einen Wert zusammenfasst, gehen gleichzeitig die Information über die Einzelwerte verloren. Bei den RSS gehen die einzelnen Beiträge der Fehlerquadrate verloren. Diese müssen daher separat untersucht werden, um die RSS korrekt interpretieren zu können. Statistische Kennzahlen wie die hat values bzw. leverage, oder Cooks Distance helfen, die Beiträge der Einzelwerte korrekt einzuordnen und somit auch der richtigen Einschätzung der residual sum of squares.
Bei der analytischen Methodenvalidierung müssen neben den allgemeinen Kennzahlen auch die RSS angegeben werden, wobei in der entsprechenden Guideline einerseits (zurecht) keine Angaben zu Obergrenzen der RSS gemacht werden, andererseits die Verwendung der Residuenanalyse mit dem Wort may nicht als zwingend erforderlich dargestellt wird. Die grafische Analyse der Residuen kann in offensichtlichen Fällen ausreichend sein, jedoch ist sie nicht in der Lage, potentielle einflussreiche Datenpunkte zu ermitteln. Doch gerade diese influencial observations können die fitness-for-purpose in Bezug auf die Linearität der Methode unter Umständen in Gefahr bringen, da diese den aufgestellten linearen Zusammenhang zwischen Analytkonzentration und Signal verzerren können. Visuelle Analysen haben immer subjektiven Charakter - „scientific justification" hingegen kann nur mit objektiven Kriterien wie z.B. Cooks Distance oder ähnlichen Residuenanalyseverfahren erreicht werden.
Die residual sum of squares stellen somit bei der Auswertung von (z.B. linearen) Regressionsverfahren den Startpunkt einer interessanten Reise dar, an dessen Ende der Erkenntnisgewinn steht, was der (z.B. lineare) Zusammenhang tatsächlich Wert ist. Damit sind die residual sum of squares nicht nur für analytische Methodenvalidierung von großer Bedeutung.
RSS, leverage und Cooks Distance in Excel 2016
Vorbereitungen
In Excel 2016 lassen sich oben beschriebene Vorgehensweisen nachrechnen: In Teil 1 besprochenes Beispiel enthält die Werte aus der Publikation von Francis Anscombe [2]. Diese beinhalten das berühmte Anscombe-Quartett, das aus 4 Datensätzen besteht, die interessanterweise allesamt die gleichen statistischen Merkmale bezüglich der linearen Regression aufweisen. Verwendet sind hier die Daten aus dem ersten der vier Datensätze (Tabelle 1).
Tabelle 1: Für das Beispiel verwendeter Datensatz
| Beobachtung | X Wert |
Y Wert |
| 1 | 4 | 4,26 |
| 2 | 5 | 5,68 |
| 3 | 6 | 7,24 |
| 4 | 7 | 4,82 |
| 5 | 8 | 6,95 |
| 6 | 9 | 8,81 |
| 7 | 10 | 8,04 |
| 8 | 11 | 8,33 |
| 9 | 12 | 10,84 |
| 10 | 13 | 7,58 |
| 11 | 14 | 9,96 |
Die X und Y Werte können leicht nach Excel kopiert werden. Werden beispielsweise in Spalte A die X Werte (oder Konzentration) und in Spalte B die Y Werte (Signal) eingetragen, kann man über die Registerkarte „Daten“ und anschließend mit Klick auf „Datenanalyse“ im sich öffnenden Fenster „Regression“ auswählen. Dort trägt man die X- und Y-Bereiche der Werte ein. Anschließend setzt man noch den Haken für die Angabe der Residuen und bestätigt mit „OK“. In dem sich öffnenden neuen Sheet befinden sich folgende Angaben in folgenden Zellen:
Tabelle 2: Angabe der Merkmale in Excel zur linearen Regression
| Zelle | Wert | Formel / Symbol | |
| Multipler Korrelationskoeffizient (correlation coefficient) | B4 | 0,816 | r |
| Bestimmtheitsmaß | B5 | 0,666 | R2 (R2 = r * r) |
| Anzahl Beobachtungen | B8 | 11 | n |
| RSS (residual sum of squares) | B14 | 13,762 | RSS = ∑ εi2 = (yi - ŷi )2 |
| Achsenschnittpunkt (y-intercept) | B17 | 3,000 | Y Wert für X = 0, β0 |
| Anstieg der Geraden (slope) | B18 | 0,500 | β1 |
| Schätzwerte für Y | B25:B35 | ŷ | |
| Residuen (residuals) | C25:C35 | ε = y - ŷ |
Es bietet sich nun an, die Ausgabe der Regression mit den Originaldaten zusammenzufügen, z.B. durch Anhängen der Originaldaten zu der Ausgabe von Excel:
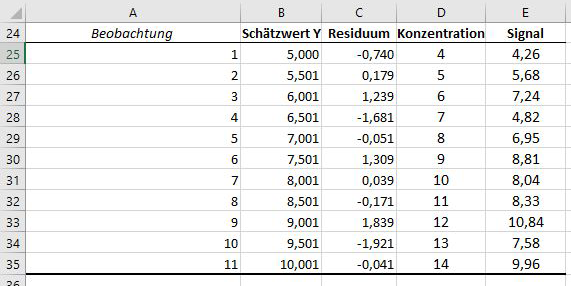
Abbildung 5: Ausgangsformat der Daten für lineare Regression und Residuenanalyse
So stehen nun die Schätzwerte für Y in Spalte B, die Residuen in Spalte C, und die originalen X und Y Werte in Spalten D und E.
Um die D Werte bzw. Cooks Distance Werte für alle Datenpunkte zu berechnen, benötigt man folgende Formel: Di = (isri2)/p * hi/(1-hi). Dabei fällt auf, dass man zwei Zwischenschritte benötigt, um D berechnen zu können. Im ersten Schritt benötigt man die Werte für den leverage, hi, und anschließend die quadrierten isr Werte. Grundlage dafür sind jedoch die residuals, aus denen sich auch die residual sum of squares berechnen lassen.
Berechnung der Residual Sum of Squares
Der Fehler, der residual, für den ersten Datenpunkt kann auch manuell über die Formel: E25 - B25 berechnet werden. Das Fehlerquadrat ergibt sich entsprechend als (E25 – B25)^2. Im Beispiel können so die manuell erstellen Residuen in Zellen F25:F35 und die Residuenquadrate in G25:G35 berechnet werden (siehe Abbildung 6). Die Summe der Residuenquadrate, die RSS beziehungsweise die residual sum of squares sind in Zelle F37 gespeichert. Der Wert von 13,76 stimmt mit dem Wert in Zelle B14 überein.
Berechnung der leverage bzw. H Werte
Für die weiteren Berechnungen benötigt man noch den Mittelwert der X Werte (x), sowie die Standardabweichung der X Werte (sx). Den Mittelwert der X Werte erhält man durch MITTELWERT(D25:D35), dieser wird in Zelle D37 gespeichert. Die Standardabweichung der X Werte erhalten wir durch STABW.S(D25:D35) und Speichern in Zelle D38. Diese Werte benötigen wir für die Berechnung des leverage bzw. der hat values:
Die Formel für die Berechnung lautet: leverage oder hi = 1/n + 1/(n-1) * ((xi-x)/sx)2. In Excel nutzt man die eben berechneten Werte für x und sx, so lautet die Formel für die Berechnung des leverage in Excel für den ersten Datenpunkt in Zelle D25: (1/$B$8) + 1/($B$8-1) * (($D25 - $D$37) / $D$38)^2. Auch hier erkennt man, dass der leverage nur von den originalen X Werten (aus der D-Spalte) und von der Lage der restlichen X Werte (aus Zellen D37 und D38) abhängig ist.
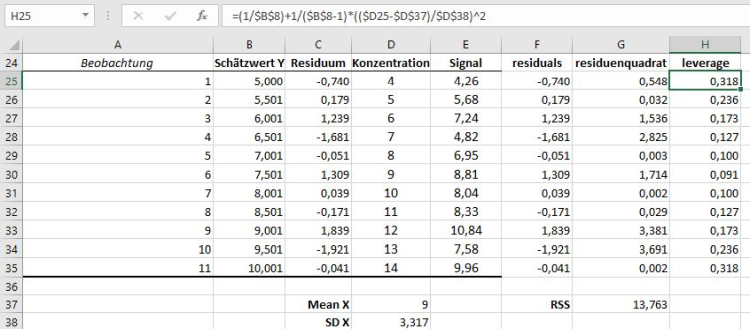
Abbildung 6: Schritte für die Berechnung des leverage
Berechnung der Cooks Distance bzw. D Werte
Den leverage benötigt man nun, um den nächsten Schritt für die Berechnung der Cooks Distance zu tätigen. Der Schritt umfasst die Berechnung eines sogenannten isr Wertes, den man für die Cooks Distance benötigt. Dieser ergibt sich aus der Formel: εi / (sE√(1-hi)). Die Werte εi für sind bereits in Spalte F bzw. Spalte C vorhanden. Die Werte für hi sind die leverage Werte in Spalte H. Den Wert SE kann man mit WURZEL(($B$8-1)/($B$8-2)*STABW.S(F25:F35)^2) bestimmen und diesen in Zelle D39 speichern. Die Formel für den ersten Datenpunkt (Reihe 25) ist daher für den isr: F25/$D$39/WURZEL(1-$H25), alle isr Werte werden in Spalte I gespeichert.
Daraus können nun im letzten Schritt die D Werte aus Cooks Distance berechnet werden. Die Distance D für Datenpunkt i ergibt sich nun als: Di = (isri2)/p * hi/(1-hi) . Für Datenpunkt 1 aus Reihe 25 ergibt sich dafür folgende Formel: $I25^2 / 2 * $H25 / (1-$H25). Die Werte werden in Spalte J gespeichert. Damit hat man nun alle Daten zusammen, um nicht nur die Regression, sondern auch die Analysis zu den Abweichungen der einzelnen Datenpunkte vornehmen zu können.
Folgende Grafik gibt nochmals eine Übersicht über alle Berechnungsschritte:
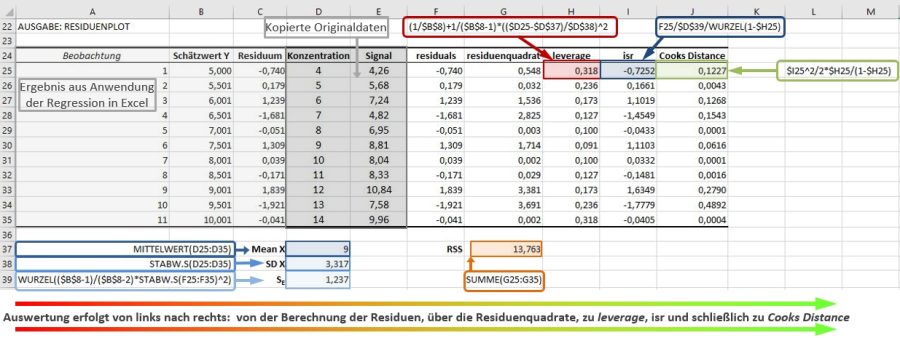
Abbildung 7: Übersicht über alle verwendeten Formeln und Zwischenschritte zur Berechnung der Cooks Distance, ausgehend von den Originaldaten, sowie dem Ergebnis der Regression in Excel 2016
Quellen
[1] Cooks Distance: Cook, R. Dennis (February 1977). "Detection of Influential Observations in Linear Regression". Technometrics. American Statistical Association. 19 (1): 15–18.
[2] Anscombes Quartett: F. J. Anscombe (1973): “Graphs in Statistical Analysis”. American Statistician. 27 (1): 17–21.
Hat Ihnen der Beitrag gefallen? Dann können Sie hier den kompletten Blogbeitrag als pdf downloaden.
Über den Autor
|
|
Dr. Peter P. Heym hat Bioinformatik studiert und am Leibnitz-Institut für Pflanzenbiochemie Halle mit dem Thema "In silico characterisation of AtPARP1 and virtual screening for AtPARP inhibitors to increase resistance to abiotic stress" (computergestütztes Inhibitordesign) promoviert. Er ist der Inhaber von Sum Of Squares - Statistical Consulting (www.sumofsquares.de), einem Dienstleistungsunternehmen, welches sich auf statistische Beratung für Studenten, Privatpersonen, Firmen und Unternehmen spezialisiert hat. Neben statistischer Beratung runden Unterstützung bei universitären Abschlussarbeiten, Betreuung und Auswertung von Umfragen, Workshops (z.B. zur Programmiersprache R), Seminare, Fortbildungen, auch im GMP-Bereich, das vielfältige Angebot ab. |

