Von kleinen Werten mit grossem Einfluss - Sum Of Squares - Teil 1
Jeder kennt diese Situation aus der eigenen, alltäglichen Arbeit: Es sind manchmal die kleinen Dinge, die einen großen Einfluss auf das Ergebnis unserer Arbeit haben können. Manchmal gewinnen unscheinbare Faktoren auf einmal an Bedeutung, wenn ihnen die entsprechende Aufmerksamkeit geschenkt wird – oder geschenkt werden muss. Einer dieser unscheinbaren Faktoren kann gerade bei der analytischen Methodenvalidierung eine große Rolle spielen.
Oft wird dieser Faktor, diese eine Zahl, übersehen, denn ihr Wert spielt bei der Validierung auf den ersten Blick keine große Rolle. Der Name dieser Zahl ist die sogenannte residual sum of squares, kurz RSS, oder zu Deutsch die „Summe der Fehlerquadrate“ [Anm. d. Red.: Es ist existiert eine Vielzahl deutscher Begrifflichkeiten, wie Residuenquadratsumme, Restquadratsumme, Restsumme der Quadrate, verbleibende Quadratsumme, Quadratsumme der Residuen, Summe der Residuenquadrate, Summe der Abweichungsquadrate oder auch Summe der quadrierten Abweichungen…]. Was es mit dieser residual sum of squares auf sich hat und wie man diese Zahl interpretiert, werden wir in diesem Beitrag am Beispiel der analytischen Methodenvalidierung klären und damit dieser Zahl die Bedeutung zukommen lassen, die sie verdient. Ebenso werden die Vor- und Nachteile der RSS besprochen, sowie Ansätze diskutiert, mit denen man potentielle Fehlinterpretationen der residual sum of squares vorbeugen kann.
Analytische Methodenvalidierung und die ICH Q2(R1)
Für die analytische Methodenvalidierung ist ein Dokument von Bedeutung, in dem mehrere Punkte einer Methode geprüft werden müssen, um sie als fit-for-purpose zu deklarieren. Fit-for-purpose bedeutet, dass die Methode den Zweck erfüllt, für den sie gedacht ist. Neben den Eigenschaften der Spezifität, des Arbeitsbereichs, der Richtigkeit und Präzision, sowie dem Bestimmen der Nachweis- und Bestimmungsgrenze (limit of detection, LOD / limit of quantification, LOQ), ist auch die Linearität der Methode zu beurteilen. Diese Eigenschaften sind in der Guideline “Validation of Analytical Procedures: Text and Methology Q2(R1)“ der ICH, des International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use, beschrieben. Für jeden dieser Punkte gelten Vorschriften, nach denen bestimmt wird, ob eine Methode fit-for-purpose ist oder nicht. Bei der Prüfung, ob eine Methode für ihren Zweck geeignet ist, orientieren sich die entsprechenden Behörden an diesem Dokument. Bei dem Thema der Linearität muss dabei nachgewiesen werden, ob es innerhalb des Arbeitsbereiches der Methode einen linearen Zusammenhang zwischen der Analytenkonzentration und einem Signal, abhängig von der verwendeten Messmethode, gibt. Die Grundlage für die Bestimmung der Linearität ist dabei das Aufstellen eines mathematischen Zusammenhangs zwischen (Analyten-) Konzentration und Signal. Der mathematische Zusammenhang kann dabei mithilfe der linearen Regression hergestellt werden, und wir können diesen anschaulich durch einfache Grafiken, wie in Abbildung 1, darstellen.
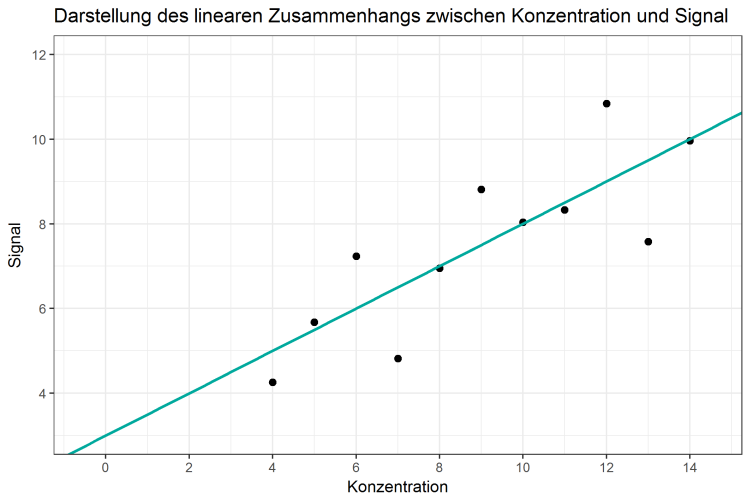
Abbildung 1: Darstellung des linearen Zusammenhangs zwischen Analytenkonzentration und Signal
Mit Hilfe solcher Darstellungen ist der Zusammenhang beider Größen erkennbar. Mit steigender Konzentration gewinnt auch das Signal an Intensität. Mathematisch wird dieser Zusammenhang durch den Anstieg der Geraden, oder auf Englisch slope, beschrieben. Was ebenfalls von Bedeutung ist, ist die Höhe der Geraden, bei der sie die y-Achse schneidet, beziehungsweise, das Signal, das bei einer Konzentration von 0 detektiert würde. Dieser Wert wird der Y-Achsenabschnitt (engl. y-intercept) genannt. Vorliegendes Beispiel weist einen Anstieg von 0,5 und einen Achsenschnittpunkt von 3,0 auf. Das bedeutet, bei einer Konzentration von 0 würde die Methode noch ein Signal von 3 detektieren und für jede Steigerung der Konzentration um eine Einheit würde sich das Signal um den Wert 0,5 erhöhen. Mathematisch lautet dieser Zusammenhang: Signal = 3 + 0,5 * Konzentration beziehungsweise y = 3 + 0,5 * x. Statistikprogramme oder Excel sind in der Lage, diese Analysen zu tätigen, darauf wird später (im Teil 2) kurz eingegangen.
Mit Blick auf die Daten stellt man fest, dass man bei einer Konzentration von 9 ein Signal von 8,81 gemessen hat. Würde man die Konzentration x = 9 in die Gleichung einsetzen, würde man jedoch einen Wert von 3 + (0,5 * 9) = 7,5 erhalten. Die Regressionsgerade sagt also etwas anderes vorher, als der Wirklichkeit entspricht. Sie beschreibt den bestmöglichen linearen Zusammenhang zwischen den Daten. Dennoch ist die Gerade nicht in der Lage, jeden Wert genau vorherzusagen, denn jeder einzelne gemessene Datenpunkt weicht von der berechneten Gerade ab. Diese Unterschiede, diese Schwankungen in den Daten, sorgen dafür, dass die Gerade den Zusammenhang nicht zu 100% erfassen kann. Sie kann in diesem Fall die Schwankungen in den gemessenen Werten zu ca. 66,7% erklären. Dieser Wert entspricht dem berühmten R2 Wert, also dem Bestimmtheitsmaß – dieser sagt aus, dass mit der berechneten Regressionsgeraden 66,7% der Variabilität in den Daten erklärt werden können. Die restlichen 33,3% an Variabilität können durch diese lineare Regression nicht erklärt werden.
Reicht eine Grafik, um der ICH Q2(R1) gerecht zu werden?
Nun sind mittels linearer Regression der lineare Zusammenhang zwischen Konzentration und Signal, als auch Anstieg und Achsenschnittpunkt, sowie die Güte des Zusammenhanges ermittelt. Reichen diese Maße aus, um unsere Methode als fit-for-purpose zu beschreiben? In der Guideline der ICH Q2(R1) heißt es dazu:
“A linear relationship should be evaluated across the range … of the analytical procedure. … Linearity should be evaluated by visual inspection of a plot of signals as a function of analyte concentration or content. If there is a linear relationship, test results should be evaluated by appropriate statistical methods, for example, by calculation of a regression line … . The correlation coefficient, y-intercept, slope of the regression line and residual sum of squares should be submitted.”
Die Regressionsgerade, zusammen mit dem slope und y-intercept, sind bereits bestimmt worden. Grafisch wurden die Daten ebenfalls dargestellt. Die Güte des Zusammenhanges wurde durch den R2 Wert ausgedrückt. Die Wurzel des R2 Wertes, die mit r bezeichnet wird, entspricht dem Korrelationskoeffizienten (correlation coefficient), der durch die ICH Q2(R1) gefordert wird. … Wäre da nicht der letzte Satz, in dem von den residual sum of squares die Rede ist.
Von Einzelwerten zu residual sum of squares
Was haben die residual sum of squares mit der Geraden und den Daten zu tun und was sagen diese eigentlich aus? Wie bereits festgestellt wurde, sagt die Gerade für die Konzentration von 9 ein Signal von 7,5 vorher, obwohl die eigentliche Messung ein Signal von 8,81 ergab. Da die Varianz in den Daten laut R2 „nur“ zu knapp 67% erklärt werden kann, bleiben noch rund 33% unerklärte Varianz übrig. Einen Teil dieser Variabilität, der Abweichung unserer Messwerte vom mathematisch idealen Zusammenhang, spiegelt sich in jedem einzelnen Messwert wider. So „verschätzt“ sich das mathematische Modell bei der Konzentration von 9 um (8,81 - 7,50) = y - ŷ = 1,31 Signaleinheiten. Das entspricht dem Fehler, den das Regressionsmodell an diesem Punkt begeht, es unterschätzt den tatsächlich gemessenen Wert von 8,81 um 1,31 Einheiten. Für die gemessene Konzentration von 8 beträgt der Unterschied zwischen Messwert und Vorhersage des Signals (6,95 – 7,00) = -0,05. Für diese Konzentration überschätzt die Gerade die tatsächliche Konzentration – wenn auch um nur 0,05 Signaleinheiten. Diesen Unterschied nennt man Fehler, Rest oder Residuum, auf Englisch error, residuum oder residual – er wird meistens mit ε (epsilon) bezeichnet. Den Fehler für den ersten Datenpunkt mit Konzentration x = 4 würde man daher folgendermaßen beschreiben: ε1 = y1 - ŷ1 = 4,26 - 5,00 = -0,74. Die Abweichungen für jeden Messwert kann man in der gleichen Grafik darstellen, indem man die entsprechenden Fehler durch graue Linien darstellt. Die Länge jeder grauen Linie entspricht dem Fehler ε, dem residual jedes Datenpunktes. Um nun die Güte des gesamten linearen Zusammenhanges zu beschrieben, liegt es auf der Hand, diese Fehler für alle Messwerte zu addieren, denn das entspräche der totalen Abweichung des linearen Modells von den gemessenen Werten:
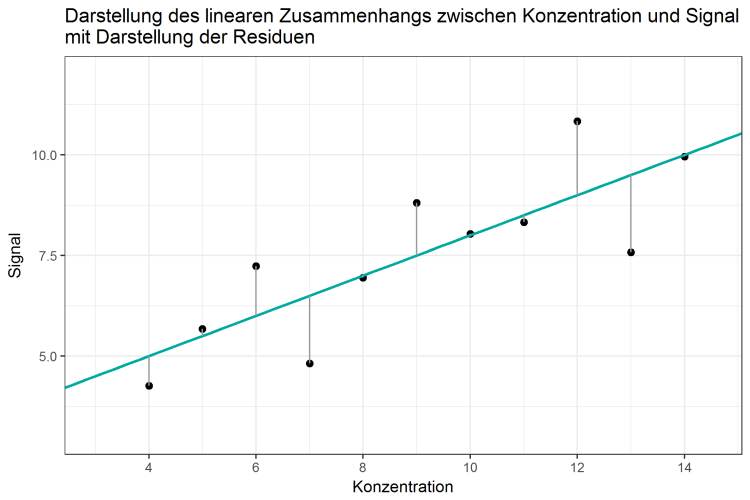
Abbildung 2: Darstellung des linearen Zusammengangs zwischen Konzentration und Signal mit Darstellung der Residuen
Wie in Tabelle 1 nachzurechnen, ist die Summe der Fehler (die sum of residuals) genau 0. Da die Abweichungen sowohl negativ, als auch positiv sein können, gleichen sich diese genau aus - dies ist eine Eigenschaft der linearen Regression. Obwohl man sehen und nachrechnen kann, dass sich das Modell in jedem Datenpunkt „verschätzt“, ist die Summe dieser Schätzfehler 0, und damit kein aussagekräftiger Wert, was die Qualität unserer Methode angeht.
Tabelle 1: Residuendarstellung
| X-Werte | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Summe |
| Residuen | -0,740 | 0,179 | 1,239 | -1,680 | -0,050 | 1,309 | 0,039 | -0,171 | 1,838 | -1,921 | -0,041 | 0 |
Um Aussagen über die Qualität machen zu können, bedient man sich daher des „Tricks“, alle Fehlerwerte zu quadrieren. Das hat zwei Vorteile: Zum einen ist das Quadrat einer Zahl immer positiv. Und zum anderen wird aus einem Wert, der kleiner als 1 ist, ein noch kleinerer Wert (z.B. 0,52 = 0,25), wohingegen Werte, die größer sind als 1, durch das Quadrieren noch größer werden (z.B. 2,52 = 6,25). Kleine Abweichungen von der Regressiongerade werden daher „belohnt“, große Abweichungen „bestraft“.
Tabelle 2: X-Werte, Residuen und Residuenquadrate des Datensatzes
| X-Werte | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Summe |
| Residuen | -0,740 | 0,179 | 1,239 | -1,680 | -0,050 | 1,309 | 0,039 | -0,171 | 1,838 | -1,921 | -0,041 | 0 |
| Residuen-quadrate | 0,547 | 0,032 | 1,535 | 2,822 | 0,002 | 1,713 | 0,001 | 0,029 | 3,378 | 3,690 | 0,001 | 13754 |
Man quadriert daher zuerst die Abweichungen, die Residuen, und summiert diese anschließend. … First, we square the residuals and sum them up afterwards. Das Ergebnis ist die Summe der Fehlerquadrate, Residuenquadratsumme oder engl. residual sum of squares. Dies ist der Wert, der beschreibt, wie groß die komplette quadratische Abweichung der Messwerte von den idealen Werten der Regressionsgerade ist. Da alle Fehler quadriert und damit positiv sind, ist auch die Summe immer positiv – kleine Summen der Fehlerquadrate sollten folglich immer gute mathematische Zusammenhänge beziehungsweise gute Kalibriergeraden, wie in diesem Beispiel, repräsentieren.
Doch was sagt der Wert über die Daten und Güte des linearen Zusammenhanges aus? Je kleiner dieser Wert ist, desto besser sollte der Zusammenhang zwischen X und Y Werten, zwischen Analytkonzentration und Signal, sein. Oder etwa doch nicht? Welche Informationen stehen in der Guideline dazu? In der ICH Q2(R1) findet sich keine Aussage bezüglich der (z.B. maximal erlaubten) Größe der residual sum of squares. Warum? Sollte es nicht Grenzen geben, die vorschreiben, was ein gutes oder erlaubtes Maß für Abweichungen ist und was nicht? Ab welchen Werten ist die Methode nicht mehr fit-for-purpose bezüglich der Linearität? Warum gibt diese Guideline keine Vorschläge oder Hinweise bezüglich der Bewertung der RSS?
Um das zu beantworten, muss man nochmals untersuchen, was die residual sum of squares bedeuten. Die sum of squares repräsentieren Abweichungen der Messwerte von den „idealen“ Werten der Regressionsgeraden. In diesem Beispiel misst man, wie in Grafik 1, das Signal in Litern. Was passiert, wenn das Signal stattdessen in Gallonen (1 Gallone = 4,54609 L) gemessen würde?
Tabelle 3: Auftretende Unterschiede in Kennzahlen der linearen Regression bei Änderung der Einheit des Signals
| Anstieg der Geraden | Achsenabschnitt | RSS | R2 | |
| Liter | 0,500 | 3,000 | 13,754 | 0,667 |
| Gallonen | 0,109 | 0,660 | 0,666 | 0,667 |
| Umrechnung | 0,5 = 0,109 * 4,54609 | 3,0 = 0,66 * 4,54609 | 13,754 = 0,666 * 4,546092 |
Der Wechsel der Einheit bewirkt mehrere Änderungen in Werten, die bei der Methodenvalidierung angegeben werden müssen. Der Achsenabschnitt verringert sich ebenso wie der Anstieg der Geraden. Die RSS reduzieren sich von über 13 auf unter 1 - auf unter 5% des originalen Wertes (!). Lediglich der R2 Wert bleibt gleich. Wie kommt dies zu Stande? Die Antwort liegt in der Umrechnung von Liter auf Gallonen. Der Umrechnungsfaktor von 4,54609 verursacht nicht nur eine Änderung der Regressionsgeraden, sondern verändert auch die residual sum of squares, obwohl die Gesamtqualität des Modelles bezogen auf den R2 Wert, wie in Tabelle 3 beschrieben, die Gleiche bleibt. Eine entsprechende Grafik bliebe bis auf die Achseneinteilung ebenfalls unverändert.
Dies bedeutet, man könnte jede beliebige (z.B. von der ICH Q2(R1) festgelegte) Obergrenze für die RSS mit Hilfe einer einfachen Änderung der Einheit elegant umgehen. Die RSS können daher immer nur in Verbindung mit der Messmethode, dem R2 und den Eigenschaften der Regressionsgeraden begutachtet werden. Die alleinige RSS hat ohne Bezug zum Rest der Methode keine Aussagekraft. Es macht also durchaus Sinn, dass die ICH die Angabe der RSS verlangt ohne eine Grenze für die Güte des Modelles festzulegen. Da die RSS nur mit allen anderen Angaben zum Regressionsmodell Sinn macht, ist auch der folgende Satz der ICH Q2(R1) völlig berechtigt:
“The … residual sum of squares should be submitted. A plot of the data should be included. In addition, an analysis of the deviation of the actual data points from the regression line may also be helpful for evaluating linearity.”
Dieser Satz ist von großer Bedeutung, auch wenn das Wort may aus der Guideline nicht sofort darauf hindeutet. Denn selbst bei kleinen RSS ist es theoretisch möglich, dass wenige Datenpunkte für einen Großteil der Abweichungen verantwortlich sind und damit die Qualität unter Umständen negativ beeinflussen. Ebenso können vermeintlich große RSS zu hervorragenden Regressionen gehören, je nachdem in welcher Einheit man misst. Dazu kommt, dass die RSS nur eine Angabe über die Abweichungen aller Datenpunkte, also z.B. der Kalibrierung über den gesamten Konzentrationsbereich, macht. Dabei müsste man darüber hinaus bewerten, wie die Beiträge der einzelnen Datenpunkte in Bezug auf die Gesamtabweichung sind. Daher wünscht sich die ICH Q2(R1) zusätzliche Maßnahmen, die neben der RSS auch die einzelnen Datenpunkte auf Einfluss untersuchen.
Um die Methode als fit-for-purpose zu deklarieren, ist es nötig, nachzuweisen, dass alle aufgenommenen Datenpunkte dem tatsächlichen chemischen oder physikalischen Zusammenhang entsprechen, daher sollten in dem Datensatz keine ungewöhnlichen Abweichungen der einzelnen Datenpunkte zu der Regressionsgeraden auftreten. Weder kleine residual sum of squares, noch hohe R2 Werte allein sind Hinweise auf fit-for-purpose Methoden. Daher muss man von Eigenschaften des Gesamtdatensatzes zu den Eigenschaften der Einzelwerte übergehen, zur „analysis of the deviation of the actual data points from the regression line“, wie es die ICH Q2(R1) fordert.
Von den residual sum of squares zu den Einzelwerten
Da die RSS nur den gesamten Datensatz betrachtet, könnte man in einem ersten Schritt für jeden Datenpunkt dessen Anteil an der residual sum of squares berechnen und dies tabellarisch oder grafisch darstellen:
Tabelle 4: Anteile der residual sum of squares bezogen auf alle Einzeldatenpunkte
| X-Werte | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Summe |
| Residuen | -0,740 | 0,179 | 1,239 | -1,680 | -0,050 | 1,309 | 0,039 | -0,171 | 1,838 | -1,921 | -0,041 | 0 |
| Residuen-quadrate | 0,547 | 0,032 | 1,535 | 2,822 | 0,002 | 1,713 | 0,001 | 0,029 | 3,378 | 3,690 | 0,001 | 13754 |
| Anteil an RSS (%) | 3,98 | 0,23 | 11,16 | 20,52 | 0,01 | 12,45 | 0,01 | 0,21 | 24,56 | 26,82 | 0,01 | 100 |
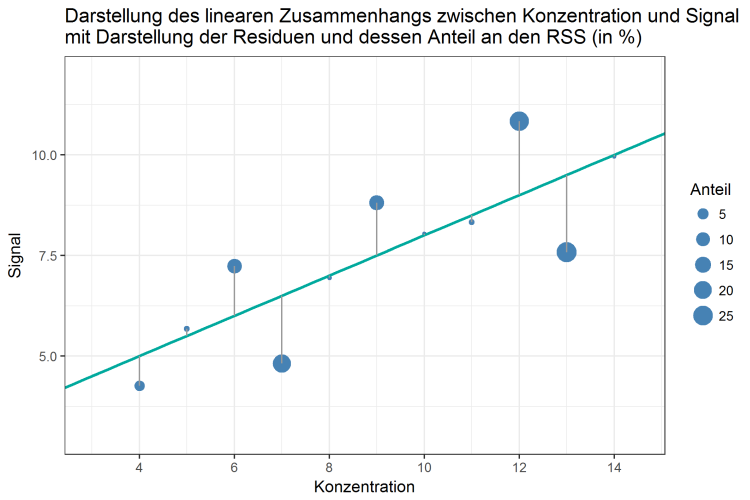
Abbildung 3: Linearer Zusammenhang zwischen Konzentration und Signal, mit Darstellung der Anteile an der residual sum of squares
In Abbildung 3 beschreibt die Größe jedes Datenpunktes den Anteil an der gesamten RSS. Doch leider gibt diese Grafik keine Aufschlüsse darüber, welchen Einfluss jeder Datenpunkt auf die Qualität des linearen Models und damit die Qualität der analytischen Methode hat. Denn obwohl bereits 3 Datenpunkte (Konzentration 7, 12 und 13) mehr als 70% der gesamten residual sum of squares ausmachen, kann man daraus nicht schlussfolgern, dass diese einen großen Einfluss, beziehungsweise andere Datenpunkte keinen Einfluss auf das Modell haben.
Im kommenden Teil 2 dieses Beitrages erfahren Sie, wie man den Einfluss der einzelnen Datenpunkte untersucht, was es mit Hat Values und Cooks Distance auf sich hat und wie man Excel zur Berechnung einsetzen kann.
Über den Autor
|
|
Dr. Peter P. Heym hat Bioinformatik studiert und am Leibnitz-Institut für Pflanzenbiochemie Halle mit dem Thema "In silico characterisation of AtPARP1 and virtual screening for AtPARP inhibitors to increase resistance to abiotic stress" (computergestütztes Inhibitordesign) promoviert. Er ist der Inhaber von Sum Of Squares - Statistical Consulting (www.sumofsquares.de), einem Dienstleistungsunternehmen, welches sich auf statistische Beratung für Studenten, Privatpersonen, Firmen und Unternehmen spezialisiert hat. Neben statistischer Beratung runden Unterstützung bei universitären Abschlussarbeiten, Betreuung und Auswertung von Umfragen, Workshops (z.B. zur Programmiersprache R), Seminare, Fortbildungen, auch im GMP-Bereich, das vielfältige Angebot ab. |

