Was ist Linearität?

In diesem Blogartikel möchten wir den Parameter "Linearität", der für analytische Methodenvalidierungen von Relevanz ist, seine Bedeutung und seine Berechnung erläutern.

Mathematisch gesehen ist die Linearität eine Funktion von Werten, die grafisch als Gerade dargestellt werden können. Analog kann gemäß der ICH Q2(R1)-Richtlinie für Methodenvalidierung die Linearität einer analytischen Methode als ihre Fähigkeit erklärt werden, "Ergebnisse zu erzielen, die direkt proportional zur Konzentration des Analyten in der Probe sind".

Die Linearität wird oft innerhalb eines vorgegebenen Bereichs gemessen. Betrachten wir zum Beispiel eine Pflanze, die alle 6 Monate über einen Zeitraum von 3 Jahren um exakt 10 cm wächst, so dass ein „lineares Wachstum“ über diese 3 Jahre beobachtet werden kann.

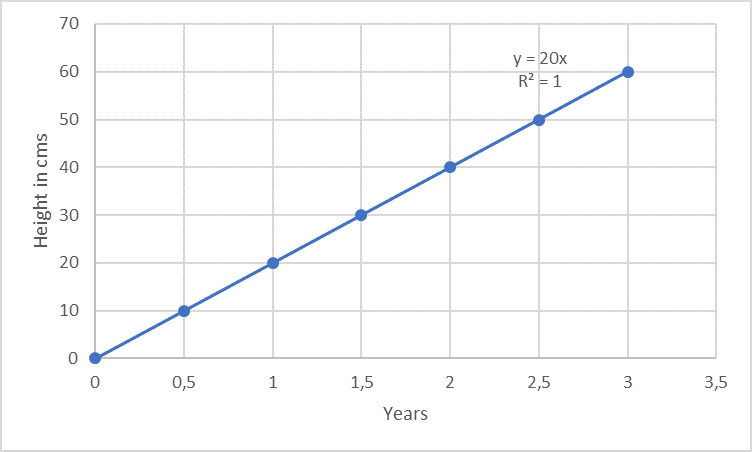
Leider ist die analytische Reaktion bei einer Methode nicht immer so ausgeprägt linear wie das Wachstum von Bäumen... (siehe Beispiel oben). Ein Beispiel aus dem analytischen Bereich ist z.B. die photometrische Proteinbestimmung nach Markwell: je mehr Protein in der Lösung vorhanden ist (also je höher die Konzentration, Variable "x"), desto stärker ist die sich entwickelnde blaue Farbe (also das Messsignal, hier: Absorption bei 650 nm, Variable "y"). Man spricht in diesem Zusammenhang auch von der abhängigen Variablen y.

Bei analytischen Methoden beispielsweise zur Analyse von Arzneimitteln oder Wirkstoffen kann die Linearität eines Signals entweder die Beziehung zwischen dem Signal des Analyten und der Konzentration des Analyten in der Kalibrierungsprobe oder die in der Probenmatrix widerspiegeln. Letzteres ist wichtiger, weil, wenn das Signal des Analyten in der Probe linear ist, es fast sicher ist, dass dies auch in den Kalibrierungsproben der Fall ist. Das Gleiche gilt jedoch nicht unbedingt für den umgekehrten Fall, zum Teil wegen des „Matrixeffekts“. Ein Matrixeffekt ist der Einfluss, der durch die anderen Komponenten der Probe (z.B. Formulierungspuffer) auf die erwartete Reaktion in Abwesenheit der zu analysierenden Substanz verursacht wird. Im Falle, dass die Daten nicht linear sind, können sie mathematisch transformiert werden, z.B. durch Logarithmieren; aber in einigen Fällen, wie beispielsweise bei Immunoassays, ist gar keine Transformation möglich. Das ist bei einem ELISA leicht verständlich, wenn man sich das zu Grunde liegende Prinzip der Methode vor Augen führt: eine definierte Anzahl an Capture-Antikörpern ist in jedem Well gebunden, welche wiederum auch nur eine bestimmte Anzahl an Zielproteinen binden können. Dies geht so lange gut (d.h. es besteht ein linearer Zusammenhang) wie noch Bindestellen frei sind. Sobald aber alle Bindestellen besetzt sind, können Unterschiede zwischen verschiedenen Proteinkonzentrationen aufgrund des Sättigungseffektes nicht mehr erfasst werden!

Die Linearität ist wichtig für die Analyse der Konzentration des Analyten im definierten Bereich. Ein definierter Bereich ist wichtig, da bei jedem Arzneimittel sowohl der Gehalt des Wirkstoffs wie auch der Gehalt potentieller Verunreinigungen von hergestellter Charge zu Charge nicht immer exakt identisch ist, sondern leicht schwanken kann, weswegen auch Konzentrationen ober- und unterhalb des jeweiligen Erwartungswertes korrekt bestimmt werden müssen. Gemäß der ICH Q2(R1)-Richtlinie für Methodenvalidierung muss die Linearität mit mindestens von 5 Konzentrationen des Analyten (Mehrpunktkalibrierung) untersucht und die Daten statistisch analysiert werden, z.B. indem eine Regressionsanalyse gemäß der Methode der kleinsten Quadrate durchgeführt wird. Dafür werden - um beim obigen Beispiel der Proteinbestimmung zu bleiben - die Konzentrationen des Analyten auf der x-Achse gegen die gemessene Absorption auf der y-Achse aufgetragen und eine Regressionsgerade durch die Punkte gelegt. Dabei bedeutet die Anwendung der kleinsten Quadrate, dass dafür die „beste“ Gerade verwendet wird. Die Ergebnisse können zusätzlich zur grafischen Darstellung in Form des Korrelationskoeffizienten R, des Y-Achsenschnittpunkts, der Steigung der Regressionsgerade und der Restsumme der Quadrate (residual sum of squares, RSS) gezeigt werden. Ein paar kurze Worte zur Residuenanalyse gibt es auch im Update am Ende dieses Beitrags. Bei der linearen Regressionsgleichung y = mx + c ist der Regressionskoeffizient die Konstante "m", welche die Änderungsrate der Variablen "y" als eine Funktion der Änderung von "x" darstellt (d.h. also bei unserem obigen Beispiel: um wieviel stärker / schwächer wird die blaue Farbe, gemessen als Absorption, wenn sich die Konzentration des Analyten ändert), während "c" der Y-Achsenabschnitt ist. Einfacher gesagt, m ist die Steigung und c ist der Ordinatenschnittpunkt. 

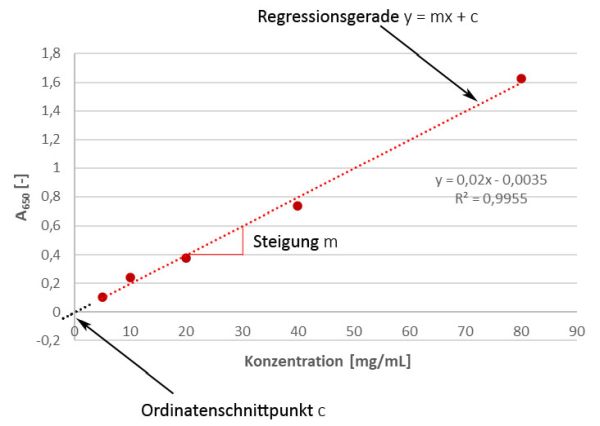
Aber was sagen uns diese beiden Größen?

• Wenn die Gerade nicht durch den Nullpunkt verläuft (was eigentlich mehr oder weniger fast immer der Fall ist), wir also einen positiven y-Wert bei einer Konzentration von 0 haben, gibt uns das einen Hinweis auf einen konstanten systematischen Fehler (Nullpunktverschiebung, Offset). Praktisch gesprochen ist das der Blank-Wert, der dann zur Korrektur abgezogen wird.
• Die Steigung hingegen gibt uns Auskunft über die Empfindlichkeit der Methode (Stichwort: „calibration sensitivity“). Es ist leicht einzusehen, dass eine steilere (also größere) Steigung mit einer größeren Empfindlichkeit einhergeht, da sie auch noch die Unterscheidung von kleinen Konzentrationsunterschieden ermöglicht. Wenn die Steigung hingegen recht flach ist, so sind kleine Konzentrationsunterschiede nicht sehr gut nachzuweisen.

Während wir mit der Regression etwas über den Zusammenhang der beiden Variablen erfahren, so gibt uns der Korrelationskoeffizient bzw. das Bestimmtheitsmaß Auskunft über die Stärke dieses Zusammenhangs. Für einen linearen Datensatz muss sich die Berechnung des Pearson-Korrelationskoeffizienten R als ausreichend erweisen. Dieser Koeffizient ist eine dimensionslose Größe, welche uns etwas über den Grad einer linearen Beziehung zwischen zwei Variablen sagt. Im Falle eines perfekt linearen Zusammenhangs hat er einen Wert von 1. Wenn der Wert kleiner als 0,95 ist, kann dies entweder das Ergebnis einer breiten Streuung während der Messung sein oder auf einer nichtlinearen Korrelation beruhen. Oft wird das Bestimmtheitsmaß (R²) verwendet, das lediglich der quadrierte Korrelationskoeffizient ist aber aufgrund der Quadrierung ein schärferes Kriterium als der Korrelationskoeffizient darstellt (siehe: R = 0,99 à R² = 0,98). Für die meisten angewandten Methoden wird mindestens ein R² ≥ 0,98 erreicht, aber es gibt keinen pauschalen, regulatorisch vorgegebenen Wert, der als Mindestmaß für eine gute Korrelation erreicht werden muss, wenngleich auch im deutschen ZLG Aide mémoire AiM 07123101 ein Korrelationskoeffizienten R von i.d.R. > 0,99 erwähnt wird. Gemäß Patric U.B. Vogel’s Trending-Büchlein sind R²-Werte zwischen 0,90 – 0,99 in der Analytik häufige Indikatoren für einen starken Zusammenhang, abhängig von der angewandten Analysenmethode. Es ist leicht verständlich, dass für gut standardisierte, chemische Methoden wie beispielsweise eine HPLC, Kalibrierkurven mit einem Bestimmtheitsmaß R² von ≥ 0,99 erhalten werden können, während für manche biologische Testsysteme R² auch deutlich niedriger ausfallen kann, was einfach durch die dem biologischen Testsystem innewohnende natürliche - im Vergleich zur chemischen HPLC - erhöhte Variabilität zu erklären ist.

Für die Validierung von Reinheitstests und Assays (unter Assays fallen Gehalts- und Wirksamkeitsbestimmungen) sind Linearitätsstudien obligatorisch. Linearitätsstudien sind wichtig, weil sie den Bereich der Methode definieren, in dem Ergebnisse genau und präzise erhalten werden können. Bei sehr kleinen zu quantifizierenden Mengen an Verunreinigungen ist eine Untersuchung der Bestimmungsgrenze (limit of quantification, LOQ) notwendig. Linearitätsexperimente am LOQ (in Kombination mit Wiederholpräzision, bei gegebener Spezifität) dienen dazu, die Richtigkeit abzuleiten, da diese auch beim LOQ gewährleistet sein muss.

 

Zusammengefasst lässt sich festhalten, dass die Linearität ein Hauptaspekt bei der Methodenvalidierung von Assays und quantitativen Bestimmungen von Verunreinigungen ist. Sie ermöglicht die Ermittlung des Konzentrationsbereichs, für den die Methode zuverlässig funktioniert. Für die Validierung werden Mehrpunktkalibrierungen akzeptiert, Einzelpunktkalibrierungen jedoch nicht. Im Falle eines nichtlinearen Datensatzes können Gleichungen höherer Ordnung transformiert werden oder die Daten müssen so wie sie sind akzeptiert werden, wobei eine eindeutige Beziehung zwischen Analytkonzentration und Signal zu zeigen ist.

 

Update: Residuenanalyse

Wie ja bereits oben erwähnt, wird die Regressionsgerade gemäß der Methode der kleinsten Quadrate gelegt. Damit ist sie eine Ausgleichsgerade und die ihr zu Grunde liegenden einzelnen Werte weichen daher alle ein klein wenig von ihr ab. Mal nach oben, mal nach unten. Veranschaulichen wir uns das doch am besten an einem Beispiel. Wir machen eine Proteinbestimmung und erhalten folgenden Datensatz:

Konz. [mg/mL]	Absorption  A650 [-]		Residuum
	gemessen	berechnet
5	0,103	0,096	0,007
10	0,240	0,196	0,044
20	0,377	0,396	-0,019
40	0,736	0,796	-0,060
80	1,624	1,595	0,029
			Σ = 0

Dabei entsprechen die „berechneten“ Werte den Werten, die wir mit Hilfe der Geradengleichung der Regressionsgerade erhalten würden, also den Idealwerten unser Regressionsgerade. Wenn wir dann den gemessenen Wert mit dem berechneten Wert verglichen (sprich: subtrahieren), erhalten wir das Residuum, also die jeweilige Abweichung. Grafisch dargestellt sieht ein Residuenplot einer solchen Residuenanalyse dann so aus:

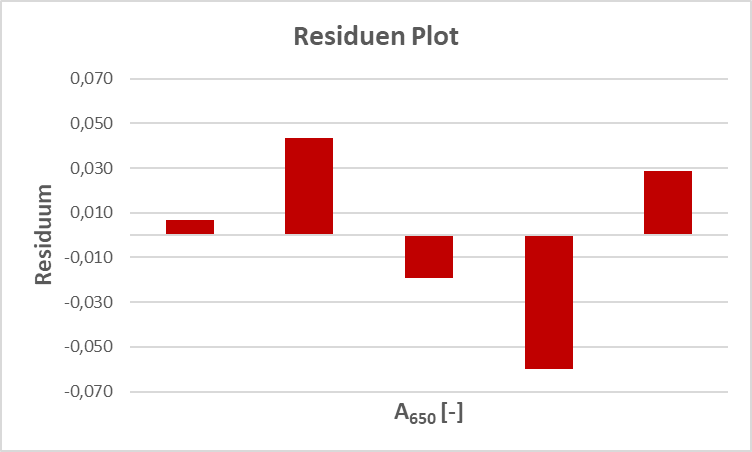
Wieviel Aussagekraft in dieser Abbildung und in einer solchen Residuenanalyse generell steckt, sei jetzt mal dahingestellt…